科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如下表):
温度 /℃ /℃ |
…… |
-4 |
-2 |
0 |
2 |
4 |
4.5 |
…… |
植物每天高度增长量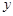 /mm /mm |
…… |
41 |
49 |
49 |
41 |
25 |
19.75 |
…… |
由这些数据,科学家推测出植物每天高度增长量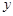 是温度
是温度 的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外两种函数的理由;
(2)温度为多少时,这种植物每天高度的增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250mm,那么实验室的温度 应该在哪个范围内选择?请直接写出结果.
应该在哪个范围内选择?请直接写出结果.
如图,在平行四边形ABCD中,AD="4" cm,∠A=60°,BD⊥AD. 一动点P从A出发,以每秒1 cm的速度沿A→B→C的路线匀速运动,过点P作直线PM,使PM⊥AD .
(1)当点P运动2秒时,设直线PM与AD相交于点E,求△APE的面积;
(2)当点P运动2秒时,另一动点Q也从A出发沿A→B→C的路线运动,且在AB上以每秒1 cm的速度匀速运动,在BC上以每秒2 cm的速度匀速运动. 过Q作直线QN,使QN∥PM. 设点Q运动的时间为t秒(0≤t≤10),直线PM与QN截平行四边形ABCD所得图形的面积为S cm2.
① 求S关于t的函数关系式;
② 求S的最大值.
已知甲乙两种食物中维生素A和B的含量及甲乙食物的成本如下表:
| 甲 |
乙 |
|
| 维生素A(单位/千克) |
300 |
500 |
| 维生素B(单位/千克) |
700 |
100 |
| 成本(元/千克) |
5 |
4 |
现将两种食物混合成100千克的混合食品。设混合食品中甲、乙食物含量分别为x(千克)和y(千克),如果混合食品中要求维生素A不低于40000单位,B不低于28000单位
(1)求x的取值范围
(2)当甲、乙各取多少千克时,符合题意的混合食品成本最低?并求该最低成本价
有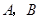 两个黑布袋,
两个黑布袋,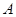 布袋中有两个完全相同的小球,分别标有数字1和2.
布袋中有两个完全相同的小球,分别标有数字1和2. 布袋中有三个完全相同的小球,分别标有数字
布袋中有三个完全相同的小球,分别标有数字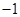 ,
,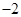 和
和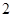 .小明从
.小明从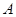 布袋中随机取出一个小球,记录其标有的数字为
布袋中随机取出一个小球,记录其标有的数字为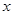 ,再从
,再从 布袋中随机取出一个小球,记录其标有的数字为
布袋中随机取出一个小球,记录其标有的数字为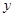 ,这样就确定点
,这样就确定点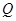 的一个坐标为
的一个坐标为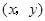 .
.
(1)用列表或画树状图的方法写出点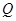 的所有可能坐标;
的所有可能坐标;
(2)求点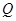 落在直线
落在直线 上的概率.
上的概率.
如图,AB是⊙O的直径,弦BC=9,∠BOC=50°,OE⊥AC,垂足为E. 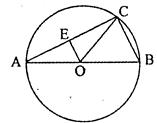
(1)求OE的长.
(2)求劣弧AC的长(结果精确到0.1).
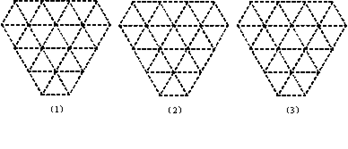
请你在下面3个网格(两相邻格点的距离均为1个单位长度)内,分别设计1个图案,要求:在图(1)中所设计的图案是面积等于 的轴对称图形;在图(2)中所设计的图案是面积等于2
的轴对称图形;在图(2)中所设计的图案是面积等于2 的中心对称图形;在图(3)中所设计的图案既是轴对称图形又是中心对称图形,并且面积等于3
的中心对称图形;在图(3)中所设计的图案既是轴对称图形又是中心对称图形,并且面积等于3 .将你设计的图案用铅笔涂黑.
.将你设计的图案用铅笔涂黑.