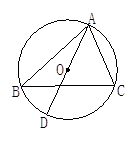吸烟有害健康,为配合“戒烟”运动,某校组织同学们在社区开展了“你支持哪种戒烟方式”的随机问卷调查,并将调查结果绘制成两幅不完整的统计图: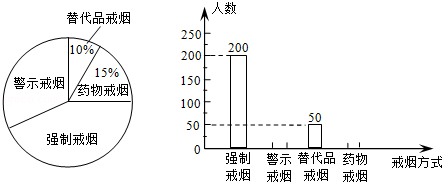
根据统计图解答下列问题:
(1)同学们一共调查了多少人?
(2)将条形统计图补充完整.
(3)若该社区有1万人,请你估计大约有多少人支持“警示戒烟”这种方式?
(4)为了让更多的市民增强“戒烟”意识,同学们在社区做了两期“警示戒烟”的宣传.若每期宣传后,市民支持“警示戒烟”的平均增长率为20%,则两期宣传后支持“警示戒烟”的市民约有多少人?
下列问题哪些是必然事件?哪些是不可能事件?哪些是随机事件?
(1)太阳从西边落山;
(2)某人的体温是50°;
(3) (其中
(其中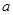 ,
, 都是实数);
都是实数);
(4)水往低处流;
(5)三个人性别各不相同;
(6)一元二次方程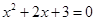 无实数解;
无实数解;
(7)经过有信号灯的十字路口,遇见红灯.
在如图中,每个正方形有边长为1 的小正方形组成: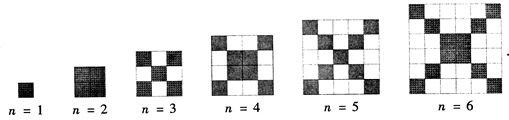
(1)观察图形,请填写下列表格:
| 正方形边长 |
1 |
3 |
5 |
7 |
… |
n(奇数) |
| 黑色小正方形个数 |
… |
|||||
| 正方形边长 |
2 |
4 |
6 |
8 |
… |
n(偶数) |
| 黑色小正方形个数 |
… |
(2)在边长为n(n≥1)的正方形中,设黑色小正方形的个数为P1,白色小正方形的个数为P2,问是否存在偶数n,使P2=5P1?若存在,请写出n的值;若不存在,请说明理由.
如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
(1)如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8平方厘米?
(2)点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积等于△ABC的面积的一半.若存在,求出运动的时间;若不存在,说明理由.
如图,△ABC是圆O的内接三角形,∠BAD是△ABC的一个外角,∠BAC,∠BAD的平分线分别交圆O于点E、F.若连接EF则EF与BC有怎样的位置关系?为什么?
如图,A、B、C、D四点都在⊙O上,AD是⊙O的直径,且AD=6cm,若∠ABC= ∠CAD,求弦AC的长.