如图有两个转盘,每个转盘都分为3个相同大小的扇形区域,分别用序号1,2,3标出.现转动两个转盘,等转盘停止转动时,指针指向每个区域的可能性相等(不计指针与两个区域交线重合的情形),将所得区域的序号相乘,比较所得积为奇数和偶数的概率的大小.有人说:因为两个转盘中奇数序号比偶数序号多,显然所得积为奇数的概率大,你同意他的说法吗?请说明理由.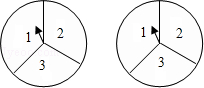
2011年徐州市全年实现地区生产总值3551.65亿元,按可比价格计算,比上年增长13.5%,经济平稳较快增长。其中,第一产业、第二产业、第三产业增加值与增长率情况如图所示: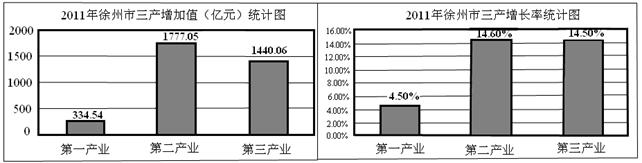
根据图中信息,写成下列填空:
(1)第三产业的增加值为 ▲亿元:
(2)第三产业的增长率是第一产业增长率的 ▲倍(精确到0.1);
(3)三个产业中第 ▲产业的增长最快。
抛掷一枚均匀的硬币2次,请用列表或画树状图的方法抛掷的结果都是反面朝上的概率。
(1)计算: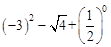 ;(2)解不等式组:
;(2)解不等式组: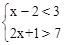 。
。
实践与探究:如图,已知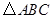 中,
中,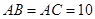 厘米,
厘米,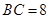 厘米,点
厘米,点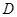 为
为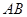 的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.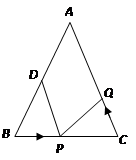
(1)用含有t的代数式表示CP
(2)若点Q的运动速度与点P的运动速度相等,经过1秒后,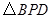 与
与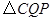 是否全等,请说明理由;
是否全等,请说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使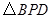 与
与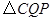 全等?
全等?
某公司每月付给销售人员的工资有两种方案.
方案一:没有底薪,只拿销售提成;方案二:底薪加销售提成(注:销售提成是指从销售每件商品得到的销售额中提取一定数量的费用).
设销售商品的数量 (件),销售人员的月工资
(件),销售人员的月工资 (元).如图所示,
(元).如图所示, 为方案一的函数图象,
为方案一的函数图象, 为方案二的函数图象.从图中信息解答如下问题:
为方案二的函数图象.从图中信息解答如下问题:
(1)求 、
、 与x的函数关系式;
与x的函数关系式;
(2)请问方案二中每月付给销售人员的底薪是多少元?
(3)如果该公司销售人员小丽当月的月工资要为1800元,那么你认为小丽选用哪种方案销售件数少些?销售件数为多少?