已知：如图1，图形①满足AD=AB，MD=MB，∠A=72°，∠M=144°．图形②与图形①恰好拼成一个菱形（如图2）．记AB的长度为a，BM的长度为b．
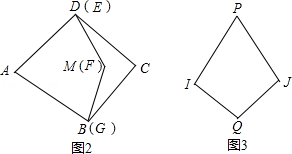
（1）图形①中∠B= °，图形②中∠E= °；
（2）小明有两种纸片各若干张，其中一种纸片的形状及大小与图形①相同，这种纸片称为“风筝一号”；另一种纸片的形状及大小与图形②相同，这种纸片称为“飞镖一号”．
①小明仅用“风筝一号”纸片拼成一个边长为b的正十边形，需要这种纸片 张；
②小明若用若干张“风筝一号”纸片和“飞镖一号”纸片拼成一个“大风筝”（如图3），其中∠P=72°，∠Q=144°，且PI=PJ=a+b，IQ=JQ．请你在图3中画出拼接线并保留画图痕迹．（本题中均为无重叠、无缝隙拼接）
某年级组织学生参加夏令营活动，本次夏令营分为甲、乙、丙三组进行。
下面两幅统计图反映了学生参加夏令营的报名情况，请你根据图中的信息回答下列问题：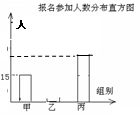
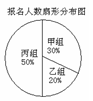
（1）该年级报名参加本次活动的总人数为人；
（2）该年级报名参加丙组的人数为人，并补全频数分布直方图；
（3）根据实际情况，需从甲组抽调部分同学到丙组，使丙组人数是甲组人数的3倍，应从甲抽调多少名学生到丙组？
如图，在边长为1的正方形组成的网格中建立直角坐标系，△AOB的顶点均在格点上，点O为原点，点A、B的坐标分别是A（3，2）、B（1，3）。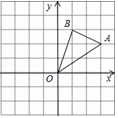
（1）将△AOB向下平移3个单位后得到△A1O1B1，则点B1的坐标为；
（2）将△AOB绕点O逆时针旋转90°后得到△A2OB2，请在图中作出△A2OB2，并求出这时点A2的坐标为；
（3）在（2）中的旋转过程中，点B经过的路径为弧BB2，那么弧BB2的长为。
如图，四边形ABCD是平行四边形，对角线AC、BD交于点O，过点O画直线EF分别交AD、BC于点E、F。求证：OE＝OF
（1）计算：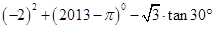
；
（2）我们已经学习了一元二次方程的四种解法：因式分解法，开平方法，配方法和公式法。请从以下一元二次方程中任选一个，并选择你认为适当的方法解这个方程。
①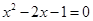
②
③
④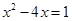
如图，抛物线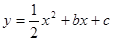
与x轴的两个交点A、B，与y轴交于点C，A点坐标为（4，0），C点坐标（0，－4）．
（1）求抛物线的解析式；
（2）用直尺和圆规作出△ＡＢＣ的外接圆⊙M，（不写作法，保留作图痕迹），并求⊙M的圆心M的坐标；