化简:2a(a﹣ )+a.
)+a.
图①、图②均为7×6的正方形网格,点A、B、C在格点上.
(1)在图①中确定格点D,并画出以A、B、C、D为顶点的四边形, 使其为轴对称图形.(画一个即可)
(2)在图②中确定格点E,并画出以A、B、C、E为顶点的四边形,使其为中心对称图形.(画一个即可)
(1)计算:2sin45°- ;
;
(2)化简:(x-1)(x+2)+ .
.
如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0),B(4,0),C(0,2)三点
(1)求这条抛物线的解析式;
(2)E为抛物线上一动点,是否存在点E使以A、B、E为顶点的三角形与△COB相似?若存在,试求出点E的坐标;若不存在,请说明理由;
某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
求销售单价为多少元时,每天的销售利润最大?最大利润是多少?
如图,A为⊙O外一点,AB切⊙O于点B,AO交⊙O于C,CD⊥OB于E,交⊙O于点D,连接OD.若AB=12,AC=8.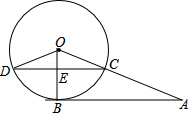
(1)求OD的长;
(2)求CD的长.