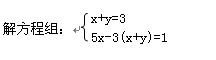为了解学生参加体育活动的情况，学校对学生进行随机抽样调查，其中一个问题是“你平均每天参加体育活动的时间是多少？”，共有4个选项（A、1.5小时以上；B、1～1.5小时；C、0.5﹣1小时；D、0.5小时以下）．并根据调查结果绘制的两幅不完整的统计图．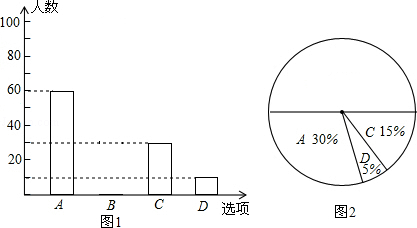
（1）参加体育活动的时间1.5小时以上的有多少人？并求出参加本次调查的学生总人数；
（2）求在这次调查中选（B）项的学生人数，并将条形统计图补充完整．
已知⊙O的直径AB的长为4㎝，C是⊙O上一点，
∠BAC=30°，过点C作⊙O的切线交AB的延长线于点
P，求BP的长
根据国务院新闻办公室2011年4月28日发布的《2011年全国第六次人口普查主要数据公报（第1号）》，就全国人口受教育情况的数据绘制了条形统计图和扇形统计图如下：
根据统计图提供的信息，解答下列问题：
（1）这次人口普查统计的全国人口总数约为亿人（精确到0.1）
（2）补全条条形统计图和扇形统计图
（3）求扇形统计图中表示“高中文化”的圆心角的度数
为了建设社会主义新农村，华新村修筑了一条长3000m的公路，实际工作效率比原计划提高了20%，结果提前5天完成任务。问原计划每天修路多长？
如图，一次函数图象与x轴交于点B，与反比例函数图象
交于点A（1，-6），△AOB的面积为6，求一次函数和反比例函
数的解析式
