观察下表三行数的规律，回答下列问题：
| |
第1列 |
第2列 |
第3列 |
第4列 |
第5列 |
第6列 |
… |
| 第1行 |
-2 |
4 |
-8 |
a |
-32 |
64 |
… |
| 第2行 |
0 |
6 |
-6 |
18 |
-30 |
66 |
… |
| 第3行 |
-1 |
2 |
-4 |
8 |
-16 |
b |
… |
(1) 第1行的第四个数a是 ；第3行的第六个数b是 ；
(2) 若第1行的某一列的数为c,则第2行与它同一列的数为 ；
(3) 已知第n列的三个数的和为2562，若设第1行第n列的数为x，试求x的值.
如图，已知直线y=x与抛物线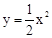
交于A、B两点．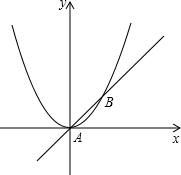
（1）求交点A、B的坐标；
（2）记一次函数y=x的函数值为y1，二次函数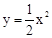的函数值为y2．若y1＞y2，求x的取值范围；
（3）在该抛物线上存在几个点，使得每个点与AB构成的三角形为等腰三角形？并求出不少于3个满足条件的点P的坐标．
如图，要建造一个直角梯形的花圃．要求AD边靠墙，CD⊥AD，AB：CD=5：4，另外三边的和为20米．设AB的长为5x米．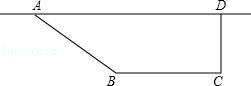
（1）请求出AD的长（用含字母x的式子表示）；
（2）若该花圃的面积为50米2，且周长不大于30米，求AB的长．
如图，抛物线y=﹣x2+4与x轴交于A、B两点，与y轴交于C点，点P是抛物线上的一个动点且在第一象限，过点P作x轴的垂线，垂足为D，交直线BC于点E．
（1）求点A、B、C的坐标和直线BC的解析式；
（2）求△ODE面积的最大值及相应的点E的坐标；
（3）是否存在以点P、O、D为顶点的三角形与△OAC相似？若存在，请求出点P的坐标，若不存在，请说明理由．
如图，过正方形ABCD的顶点D作DE∥AC交BC的延长线于点E．
（1）判断四边形ACED的形状，并说明理由；
（2）若BD=8cm，求线段BE的长．
如图，正比例函数y1=x的图象与反比例函数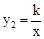
（k≠0）的图象相交于A、B两点，点A的纵坐标为2．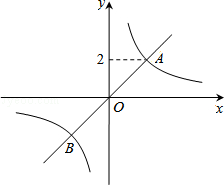
（1）求反比例函数的解析式；
（2）求出点B的坐标，并根据函数图象，写出当y1＞y2时，自变量x的取值范围．