对于点E和四边形ABCD，给出如下定义：在四边形ABCD的边AB上任取一点E（点E不与A、B重合），分别连接ED、EC，可以把四边形ABCD分成三个三角形，如果其中有两个三角形相似，则称E为四边形ABCD边AB上的“相似点”；如果这三个三角形都相似，我们称E为四边形ABCD边AB上的“强相似点”．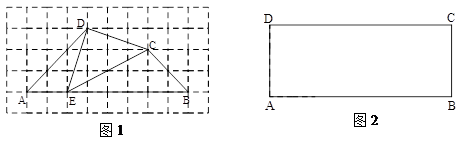 
如图1，在四边形ABCD中，A、B、C、D四点均在正方形网格（网格中每个小正方形的边长为1）的格点（即每个小正方形的顶点）上， 点E是AB边上一点，∠DEC=45°，试判断点E是否是四边形ABCD边AB上的相似点，并证明你的结论正确；
（2）如图2，在矩形ABCD中，AB=8，AD=3.
①在AB边上是否存在点E，使点E为四边形ABCD边AB上的“强相似点”．若存在，有几个？试在图2中画出所有强相似点；
②在①所画图形的基础上求AE的长.
在一次汽车车展期间，某汽车经销商推出A、B、C、D四种型号的小轿车共1000辆进行展销．C型号轿车销售的成交率为50%，其它型号轿车的参展与销售情况绘制在图1和图2两幅尚不完整的统计图中．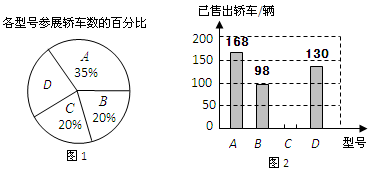
⑴ 参加展销的D型号轿车有辆；
⑵ 请你将图2的统计图补充完整；
⑶ 从成交率看，哪一种型号的轿车销售情况最好？
两个大小不同的等腰直角三角形三角板如图①所示放置，图②是由它抽象出的几何图形，B，C，E在同一条直线上，连接DC，
（1）请找出图②中的全等三角形，并给予证明（说明：结论中不得含有未标识的字母）。
（2）证明：DC⊥BE。
一次函数y=k
x+b的图像经过点（0，-4）且与正比例函数y=k
x的图象交于点（2，-1）．
（1）分别求出这两个函数的表达式；
（2）求这两个函数的图象与x轴围成的三角形的面积；
（3）直接写出不等式kx-4≥kx的解集。
已知：如图，点B、C、E在同一条直线上，AC∥DE，AC=CE，BC=DE，求证：AB=CD。
分解因式：（1）n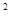
（m-2）-n（2-m）；（2）2a
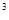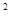-4ab+2ab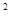；