如图,已知△OAB的顶点A(﹣6,0),B(0,2),O是坐标原点,将△OAB绕点O按顺时针旋转90°,得到△ODC.
(1)写出C,D两点的坐标;
(2)求过A,D,C三点的抛物线的解析式,并求此抛物线顶点E的坐标;
(3)证明AB⊥BE
如图,在平面直角坐标系中,直角梯形 的边
的边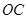 落在
落在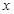 轴的正半轴上,且
轴的正半轴上,且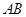 ∥
∥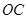 ,
,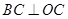 ,
,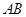 =4,
=4,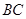 =6,
=6,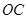 =8.正方形
=8.正方形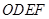 的两边分别落在坐标轴上,且它的面积等于直角梯形
的两边分别落在坐标轴上,且它的面积等于直角梯形 面积。将正方形
面积。将正方形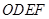 沿
沿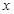 轴的正半轴平行移动,设它与直角梯形
轴的正半轴平行移动,设它与直角梯形 的重叠部分面积为
的重叠部分面积为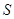 。
。
(1)分析与计算:
求正方形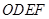 的边长;
的边长;
(2)操作与求解:
①正方形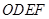 平行移动过程中,通过操作、观察,试判断
平行移动过程中,通过操作、观察,试判断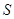 (
(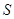 >0)的变化情况是 ;
>0)的变化情况是 ;
| A.逐渐增大 | B.逐渐减少 | C.先增大后减少 | D.先减少后增大 |
②当正方形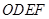 顶点
顶点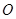 移动到点
移动到点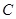 时,求
时,求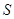 的值;
的值;
(3)探究与归纳:
|
设正方形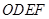 的顶点
的顶点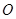 向右移动的距离为
向右移动的距离为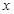 ,求重叠部分面积
,求重叠部分面积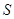 与
与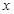 的函数关系式。
的函数关系式。

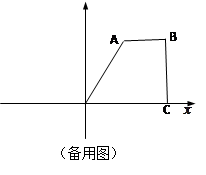
已知抛物线 与x轴交于两点
与x轴交于两点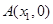 、
、
 ,与y轴交于点C,AB=6.
,与y轴交于点C,AB=6.
(1)求抛物线和直线BC的解析式.
(2)在给定的直角坐标系中,画出抛物线和直线BC.
(3)若⊙P过A、B、C三点,求⊙P的半径.
(4)抛物线上是否存在点M,过点M作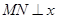 轴于点N,使
轴于点N,使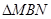 被直线BC分成面积比为
被直线BC分成面积比为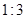 的两部
的两部
分?若存在,请求出点M的坐标;若不存在,请说明理由.
某土产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售.按计划20辆车都要装运,每辆汽车只能装运同一种圭特产,且必须装满.根据下表提供的信息,解答以下问题:
| 土特产种类 |
甲 |
乙 |
丙 |
| 每辆汽车运载量(吨) |
8 |
6 |
5 |
| 每吨土特产获利(百元) |
12 |
16 |
10 |
(1)设装运甲种土特产的车辆数为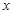 ,装运乙种土特产的车辆数为
,装运乙种土特产的车辆数为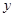 ,求
,求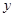 与
与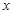 之间的函数关系式.
之间的函数关系式.
(2)如果装运每辆土特产的车辆都不少于3辆,那么车辆的安排方案有几种?并写出每种安排方案.
(3)若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值.
如图,在水平面上放置一圆锥,在圆锥顶端斜靠着一根木棒(木棒的厚度可忽略不计)
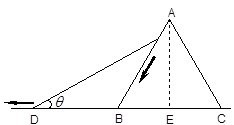
小明为了探究这个问题,将此情景画在了草稿纸上(如右图所示):运动过程:木棒顶端从A点开始沿圆锥的母线下滑,速度为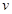 (木棒下滑为匀速)已知木棒与水平地面的夹角为
(木棒下滑为匀速)已知木棒与水平地面的夹角为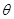 ,
,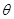 随木棒的下滑而不断减小。
随木棒的下滑而不断减小。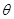 的最大值为30°,若木棒长为
的最大值为30°,若木棒长为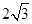
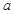 。问:当木棒顶端从A滑到B这个过程中,木棒末端的速度
。问:当木棒顶端从A滑到B这个过程中,木棒末端的速度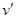 为多少?
为多少?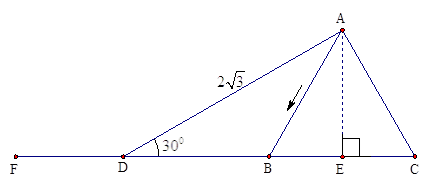
为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图,按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,为标明限高,请你根据该图计算CE.(精确到0.1m)
(下列数据提供参考: 20°=0.3420,
20°=0.3420,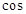 20°=0.9397,
20°=0.9397,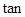 20°=0.3640)
20°=0.3640)