某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)有4张桌子,用第一种摆设方式,可以坐___________人;当有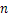 张桌子时,用第二种摆设方式可以坐___________人(用含有n的代数式表示).
张桌子时,用第二种摆设方式可以坐___________人(用含有n的代数式表示).
(2)一天中午,餐厅要接待85位顾客共同就餐,但餐厅中只有20张这样的长方形桌子可用,且每4张拼成一张大桌子,若你是这家餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?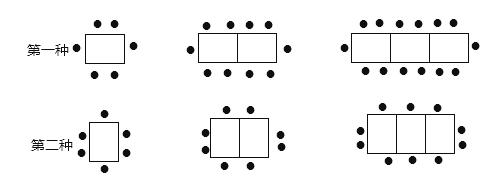
如图,一次函数 与反比例函数 的图象交于点 和 .
(1)填空:一次函数的解析式为 ,反比例函数的解析式为 ;
(2)点 是线段 上一点,过点 作 轴于点 ,连接 ,若 的面积为 ,求 的取值范围.
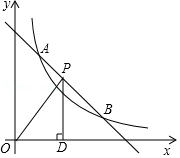
如图所示,我国两艘海监船 , 在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船 ,此时, 船在 船的正南方向5海里处, 船测得渔船 在其南偏东 方向, 船测得渔船 在其南偏东 方向,已知 船的航速为30海里 小时, 船的航速为25海里 小时,问 船至少要等待多长时间才能得到救援?(参考数据: , , ,
如图,在 中, ,以 为直径的 交 边于点 ,过点 作 ,与过点 的切线交于点 ,连接 .
(1)求证: ;
(2)若 , ,求 的长.

为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
调查结果统计表
|
组别 |
分组(单位:元) |
人数 |
|
|
|
4 |
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
2 |
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有 人, , ;
(2)求扇形统计图中扇形 的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额 在 范围的人数.

如图1,在平面直角坐标系中,抛物线 与直线 交于点 和点 ,与 轴交于点 .
(1)求 , 的值及抛物线的解析式;
(2)在图1中,把 平移,始终保持点 的对应点 在抛物线上,点 , 的对应点分别为 , ,连接 ,若点 恰好在直线 上,求线段 的长度;
(3)如图2,在抛物线上是否存在点 (不与点 重合),使 和 的面积相等?若存在,直接写出点 的坐标;若不存在,请说明理由.
