某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价25元/件时,每天的销售量是250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式.
(2)求销售单价为多少元时,该文具每天的销售利润最大?
(3)商场的营销部结合上述情况,提出了A,B两种营销方案:方案A:该文具的销售单价高于进价且不超过30元;方案B:每天销售量不少于10件,且每件文具的利润至少为25元.请比较哪种方案的最大利润更高,并说明理由.
（本题8分）小敏上午8：00从家里出发，骑车去一家超市购物，然后从这家超市返回家中．小敏离家的路程
（米）和所经过的时间
之间的函数图象如图所示．请根据图象回答下列问题：
（1）小敏去超市途中的速度是多少？在超市逗留了多少时间？
（2）小敏几点几分返回到家？
（本题8分）
（1）计算：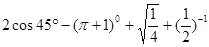
；
（2）解不等式：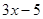
≤
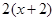
定义：如图1，点M，N把线段AB分割成AM，MN和BN，若以AM，MN，BN为边的三角形是一个直角三角形，则称点M，N是线段AB的勾股分割点
（1）已知点M，N是线段AB的勾股分割点，若AM=2，MN=3求BN的长；
（2）如图2，在△ABC中，FG是中位线，点D，E是线段BC的勾股分割点，且EC>DE≥BD，连接AD，AE分别交FG于点M，N，求证：点M，N是线段FG的勾股分割点
（3）已知点C是线段AB上的一定点，其位置如图3所示，请在BC上画一点D，使C，D是线段AB的勾股分割点（要求尺规作图，保留作图痕迹，画出一种情形即可）
（4）如图4，已知点M，N是线段AB的勾股分割点，MN>AM≥BN，△AMC，△MND和△NBM均是等边三角形，AE分别交CM，DM，DN于点F，G，H，若H是DN的中点，试探究
，
和
的数量关系，并说明理由
如图，在多边形ABCDE中，∠A=∠AED=∠D=90°，AB=5，AE=2，ED=3，过点E作EF∥CB交AB于点F，FB=1，过AE上的点P作PQ∥AB交线段EF于点O，交折线BCD于点Q，设AP=x，PO．OQ=y
（1）①延长BC交ED于点M，则MD=，DC=
②求y关于x的函数解析式；
（2）当
时，
，求a，b的值；
（3）当
时，请直接写出x的取值范围
如图，四边形ABCD内接于⊙O，点E在对角线AC上，EC=BC=DC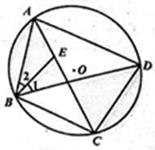
（1）若∠CBD=39°，求∠BAD的度数
（2）求证：∠1=∠2