定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点
(1)已知点M,N是线段AB的勾股分割点,若AM=2,MN=3求BN的长;
(2)如图2,在△ABC中,FG是中位线,点D,E是线段BC的勾股分割点,且EC>DE≥BD,连接AD,AE分别交FG于点M,N,求证:点M,N是线段FG的勾股分割点
(3)已知点C是线段AB上的一定点,其位置如图3所示,请在BC上画一点D,使C,D是线段AB的勾股分割点(要求尺规作图,保留作图痕迹,画出一种情形即可)
(4)如图4,已知点M,N是线段AB的勾股分割点,MN>AM≥BN,△AMC,△MND和△NBM均是等边三角形,AE分别交CM,DM,DN于点F,G,H,若H是DN的中点,试探究 ,
, 和
和 的数量关系,并说明理由
的数量关系,并说明理由

如图,已知正方形ABCD,点P为射线BA上的一点(不和点A,B重合),过P作PE⊥CP,且CP=PE.过E作EF∥CD交射线BD于F.若CB=6,PB=2,则EF=;DF=;
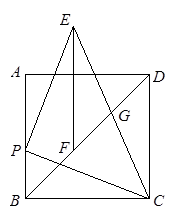
请探究BF,DG和CD这三条线段之间的数量关系,写出你的结论并证明;
如图2,点P在线段BA的延长线上,当tan∠BPC=时,四边形EFCD与四边形PEFC的面积之比为
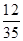 .
.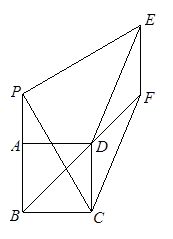
如图1,已知抛物线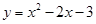 与x轴交于点A和点B,与y轴相交于点C.
与x轴交于点A和点B,与y轴相交于点C.求A、B、C三点的坐标
点D为射线CB上的一动点(点D、B不重合),过点B作x轴的垂线BE与以点D为顶点的抛物线y=(x-t)2+h相交于点E,从△ADE和△ADB中任选一个三角形,求出当其面积等于△ABE的面积时的t的值;(友情提示:1、只选取一个三角形求解即可;2、若对两个三角形都作了解答,只按第一个解答给分.)
如图2,若点P是直线
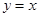 上的一个动点,点Q是抛物线上的一个动点,若以点O,C,P和Q为顶点的四边形为直角梯形,求相应的点P的坐标.
上的一个动点,点Q是抛物线上的一个动点,若以点O,C,P和Q为顶点的四边形为直角梯形,求相应的点P的坐标.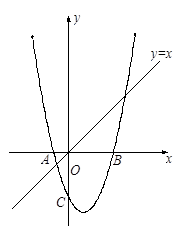
某跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动路线是如图所示坐标系下经过原点O的一条抛物线(图中标出的数据为已知条件).在跳某个规定动作时,正常情况下,该运动员在空中的最高处距水面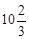 米,入水处距池边的距离为4米,运动员在距水面高度为5米以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
米,入水处距池边的距离为4米,运动员在距水面高度为5米以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.求这条抛物线的解析式;
在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中完成规定的翻腾动作并调整好入水姿势时,距池边的水平距离为
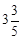 米,问此次跳水会不会失误?并通过计算说明理由.
米,问此次跳水会不会失误?并通过计算说明理由.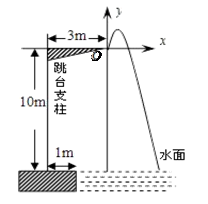
如图,AB为⊙O的直径,AM和BN是它的两条切线,E为⊙O的半圆弧上一动点(不与A、B重合),过点E的直线分别交射线AM、BN于D、C两点,且CB=CE.
求证:CD为⊙O的切线
若tan∠BAC=
 ,求 的值
,求 的值
如图,网格中每个小正方形的边长都是1个单位.折线段ABC的位置如图所示.现把折线段ABC向右平移4个单位,画出相应的图形
 ;
;把折线段
 绕线段
绕线段 的中点D顺时针旋转90°,画出相应的图形
的中点D顺时针旋转90°,画出相应的图形
在上述两次变换中,点
 的路径的长度比点
的路径的长度比点 的路径的长度大 个单位.
的路径的长度大 个单位.