(本小题满分16分)在数列  中,已知
中,已知  ,
, 为常数.
为常数.
(1)证明:  成等差数列;
成等差数列;
(2)设  ,求数列 的前n项和
,求数列 的前n项和  ;
;
(3)当 时,数列
时,数列  中是否存在三项
中是否存在三项  成等比数列,且
成等比数列,且 也成等比数列?若存在,求出
也成等比数列?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
设U=R,A={ },B={
},B={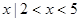 },求
},求
(1)∁UB;(2)当B⊆A时,求 的取值范围.
的取值范围.
(1)求值: ; (2)已知
; (2)已知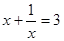 求
求 的值
的值
(本小题满分13分)经市场调查,某商场的一种商品在过去的一个月内(以30天计)销售价格 (元)与时间
(元)与时间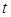 (天)的函数关系近似满足
(天)的函数关系近似满足 (
(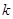 为正的常数),日销售量
为正的常数),日销售量 (件)与时间
(件)与时间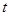 (天)的函数关系近似满足
(天)的函数关系近似满足 ,且第25天的销售金额为13000元.
,且第25天的销售金额为13000元.
(1)求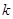 的值;
的值;
(2)试写出该商品的日销售金额 关于时间
关于时间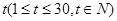 的函数关系式,并求前半个月销售金额
的函数关系式,并求前半个月销售金额 的最小值。
的最小值。
(本小题满分13分)已知函数 的图象经过点(2,
的图象经过点(2,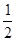 ),其中
),其中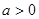 且
且 。
。
(1)求 的值;
的值;
(2)若函数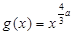 ,解关于
,解关于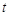 的不等式
的不等式 。
。
(本小题满分12分)
已知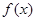 是定义在
是定义在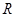 上的奇函数,当
上的奇函数,当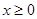 时,
时,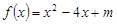 。
。
(1)求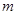 及
及 的值;
的值;
(2)求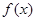 的解析式并画出简图;
的解析式并画出简图;
(3)写出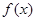 的单调区间(不用证明)。
的单调区间(不用证明)。