如果函数 对定义域
对定义域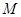 内的任意两个不相等的实数
内的任意两个不相等的实数 ,都有
,都有 ,则称函数
,则称函数 在定义域
在定义域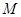 内为“
内为“ ”函数.给出函数:
”函数.给出函数:
① ;
;
② ;
;
③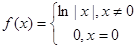 ;
;
④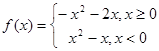 .
.
以上函数为“ ”函数的序号是 .
”函数的序号是 .
类比“两角和与差的正弦公式”的形式,对于给定的两个函数: ,
,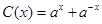 ,其中
,其中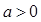 ,且
,且 ,下面正确的运算公式是()
,下面正确的运算公式是()
① ; ②
; ②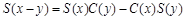 ;
;
③2 ; ④2
; ④2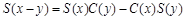 .
.
| A.①② | B.③④ | C.①④ | D.②③ |
函数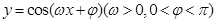 为奇函数,该函数的部分图像如右图所示,
为奇函数,该函数的部分图像如右图所示, 、
、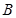 分别为最高点与最低点,且
分别为最高点与最低点,且
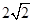 ,则该函数图象的一条对称轴为()
,则该函数图象的一条对称轴为()
A.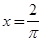 |
B.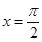 |
C.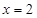 |
D. 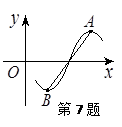 |
在平面直角坐标系中,若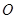 为坐标原点,则
为坐标原点,则 、
、 、
、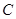 三点在同一直线上的等价条件为存在唯一的实数
三点在同一直线上的等价条件为存在唯一的实数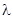 ,使得
,使得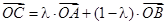 成立,此时称实数
成立,此时称实数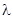 为“向量
为“向量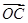 关于
关于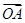 和
和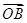 的终点共线分解系数”.若已知
的终点共线分解系数”.若已知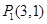 、
、 ,且向量
,且向量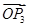 与向量
与向量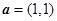 垂直,则“向量
垂直,则“向量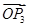 关于
关于 和
和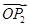 的终点共线分解系数”为()
的终点共线分解系数”为()
A. |
B.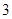 |
C.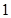 |
D.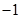 |
下列各式中,值为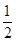 的是()
的是()
A.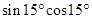 |
B.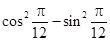 |
C. |
D.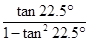 |
已知 为锐角,
为锐角, ,则
,则 =()
=()
A. |
B. |
C. |
D. |