大润发超市以每件30元的价格购进一种商品，试销中发现每天的销售量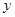
（件）与每件的销售价
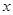（元）之间满足一次函数
.
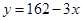（1）写出超市每天的销售利润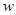
（元）与每件的销售价x（元）之间的函数关系式；
（2）如果超市每天想要获得销售利润420元，则每件商品的销售价应定为多少元？
（3）如果超市要想获得最大利润，每件商品的销售价定为多少元最合适？最大销售利润为多少元？
已知关于x的方程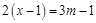
与
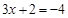的解互为相反数，求m的值．
化简求值：5a2＋3b2＋2（a2－b2）－（5a2－3b2），其中
．
解方程：
（1）4－x＝2－3（2－x）；
（2）
－
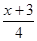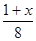＝1．
某单位急需用车，但又不需买车，他们准备和一个个体车主或一国营出租公司中的一家签定月租车合同，个体车主的收费是3元/千米，国营出租公司的月租费为2000元，另外每行驶1千米收2元，这个单位若每月平均跑1500千米，租用哪个公司的车比较合算？每月跑多少千米两家公司的费用一样?
如图，M是线段AC的中点，N是线段BC的中点．
（1）如果AC=8cm，BC=6cm，求MN的长．
（2）如果AM=5cm，CN=2cm，求线段AB的长．