如图,二次函数的图象与x轴交与A(4,0),并且OA=OC=4OB,点P为过A、B、C三点的抛物线上一动点.
(1)求点B、点C的坐标并求此抛物线的解析式;
(2)是否存在点P,使得△ACP是以点C为直角顶点的直角三角形?若存在,求出点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
如图,在图a、图b、图c中都有直线m∥n,
(1)在图a中,∠2和∠1、∠3之间的数量关系是.
(2)猜想:在图b中,∠1、∠2、∠3、∠4之间的数量关系是。
(3)猜想:在图c中,∠2、∠4和∠1、∠3、∠5的数量关系式是 。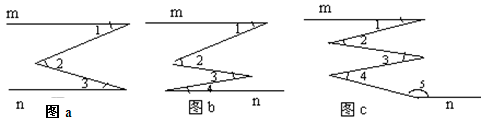
某天早晨,小王从家出发,骑摩托车前往工厂上班,途中在路旁一家饭店吃早餐,如图所示的是小王从家到工厂这一过程中行驶路程 s(千米)与时间t之间的关系.
(1)工厂离小王家多远?从家出发到工厂,小王共用了多少时间?
(2)小王吃早餐用了多少时间?
(3)小王吃早餐以前的速度快还是吃完早餐以后的速度快?最快时速达到多少?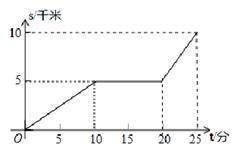
先化简,后求值: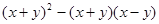 ,其中
,其中 ,
,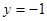 。
。
已知∠ABC,点P在射线BA上,请根据“同位角相等,两直线平行”,利用直尺和圆规,过点P作直线PD平行于BC。(保留作图痕迹,不写作法。)
利用平方差公式或完全平方公式进行简便计算:
(1)203×197(2)1022