如图,抛物线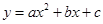 (
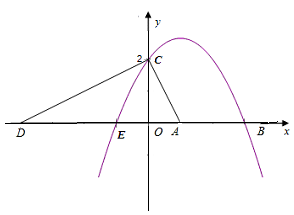
( )与x轴相交于两点E、B(E在B的左侧),与y轴相交于点C(0,2),点D的坐标为(-4,0),且AB=AE=2,
)与x轴相交于两点E、B(E在B的左侧),与y轴相交于点C(0,2),点D的坐标为(-4,0),且AB=AE=2,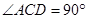 .
.
(1)求点A、B、E的坐标;
(2)求抛物线的解析式;
(3)在第一象限的抛物线上,是否存在一点M,作MN⊥x轴,垂足为N,使得以M、N、O为顶点的三角形与△AOC相似.
某校教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行了调查统计,并绘制了下表
| 零花钱数额/元 |
5 |
10 |
15 |
20 |
| 学生人数 |
10 |
15 |
20 |
5 |
(1)求出这50名学生每人一周内的零花钱数额的平均数、众数和中位数;
(2)你认为(1)中的哪个数据代表这50名学生每人一周零花钱数额的一般水平较为合适?简要说明理由.
如图:在每个小正方形的边长为1个单位长度的方格纸中,有一个△ABC和点O,△ABC的各顶点和O点均与小正方形的顶点重合.
(1)在方格纸中,将△ABC向下平移5个单位长度得△A1B1C1,请画出△A1B1C1;
(2)在方格纸中,将△ABC绕点O顺时针旋转180°得到△A2B2C2,请画出△A2B2C2.
(1)计算 ;
;
(2)化简 ;
;
(3)解方程组
你能很快算出20052吗?为了解决这个问题,我们考察个位上的数字是5的自然数的平方,任意一个个位数为5的自然数可写成10n+5,即求(10n+5)2的值(为正整数),请分析n=1,n=2,……这些简单情况,从中探索其规律,并归纳、猜想出结论(在下面的空格内填上你探索的结果)
(1)通过计算,探索规律:
152=225可写成100×1×(1+1)+25
252=625可写成100×2×(2+1)+25
352=1225可写成100×3×(3+1)+25
452=2025可写成100×4×(4+1)+25
……
752=5625可写成
852=7225可写成;
(2)从小题(1)的结果归纳、猜想得:(10n+5)2=;
(3)根据上面的归纳、猜想,请计算出:20052 =.
如图,四边形ABCD中,∠A=90°。,连结对角线BD,BD⊥BC,现测得AB=9cm,AD=12cm,CD=17cm,求四边形ABCD的面积.