在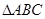 中,内角
中,内角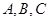 对边分别为
对边分别为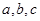 ,且
,且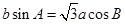 .
.
(Ⅰ)求角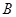 的大小;
的大小;
(Ⅱ)若 ,求
,求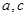 的值.
的值.
已知实数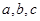 成等差数列,
成等差数列,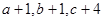 成等比数列,且
成等比数列,且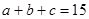 。
。
求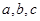 。
。
设等比数列 的前
的前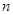 项和为
项和为 ,若
,若 ,求公比
,求公比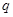 。
。
某同学要把自己的计算机接入因特网,现有两家ISP公司可供选择,公司A每小时受费1.5元;公司B的收费规则如下:在用户上网的第1小时内收费1.7元,第2小时内收费1.6元,以后每小时减少0.1元(若超过17小时,按17小时计算)如图所示.
假设一次上网时间总小于17小时,那么,一次上网在多长时间以内能够保证选择公司A比选择公司B所需费用少?请写出其中的不等关系.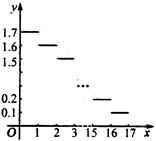
某蔬菜收购点租用车辆,将100t新鲜辣椒运往某市销售,可租用的大卡车和农用车分别为10辆和20辆,若每辆卡车载重8t,运费960元,每辆农用车载重2.5t,运费360元,据此,安排两种车型,应满足那些不等关系,请列出来.
某旅游公司年初以98万元购进一辆豪华旅游车,第一年各种费用为12万元,以后每年都增加4万元,该车每年的旅游效益为50万元,设第n年开始获利,列出关于n的不等关系.