(本小题满分12分)如图,在四棱锥 中,
中, 平面
平面 ,
, ,四边形
,四边形 满足
满足 ,
, 且
且 ,点
,点 为
为 中点,点
中点,点 为
为 边上的动点,且
边上的动点,且 .
.
 求证:平面
求证:平面 平面
平面 ;
; 是否存在实数
是否存在实数 ,使得二面角
,使得二面角 的余弦值为
的余弦值为 ?若存在,试求出实数
?若存在,试求出实数 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知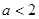 ,函数
,函数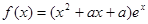
(1)当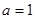 时,求
时,求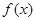 的单调递增区间;
的单调递增区间;
(2)若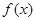 的极大值是
的极大值是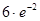 ,求
,求 的值.
的值.
已知函数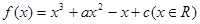 ,下列结论错误的是()
,下列结论错误的是()
A.函数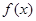 一定存在极大值和极小值 一定存在极大值和极小值 |
B.若函数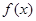 在 在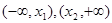 上是增函数,则 上是增函数,则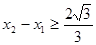 |
C.函数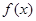 的图像是中心对称图形 的图像是中心对称图形 |
D.函数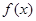 一定存在三个零点 一定存在三个零点 |
已知函数f(x)=-x3+ax2+1(a∈R).
(1)若函数y=f(x)在区间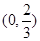 上递增,在区间
上递增,在区间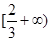 上递减,求a的值;
上递减,求a的值;
(2)当x∈[0,1]时,设函数y=f(x)图象上任意一点处的切线的倾斜角为θ,若给定常数a∈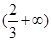 ,求
,求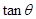 的取值范围;
的取值范围;
(3)在(1)的条件下,是否存在实数m,使得函数g(x)=x4-5x3+(2-m)x2+1(m∈R)的图象与函数y=f(x)的图象恰有三个交点.若存在,求实数m的取值范围;若不存在,试说明理由.
在平面直角坐标系 中,点P到两点(0,-
中,点P到两点(0,-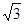 )、(0,
)、(0,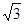 )的距离之和等于4.设点P的轨迹为C.
)的距离之和等于4.设点P的轨迹为C.
(1)写出C的方程;
(2)设直线y=kx+1与C交于A、B两点.k为何值时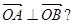 此时|
此时|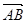 |的值是多少?
|的值是多少?
如图,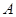 是以
是以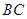 为直径的⊙O上一点,
为直径的⊙O上一点, 于点
于点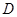 ,过点
,过点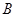 作⊙O的切线,与
作⊙O的切线,与 的延长线相交于点
的延长线相交于点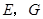 是
是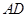 的中点,连结
的中点,连结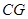 并延长与
并延长与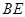 相交于点
相交于点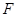 ,延长
,延长 与
与 的延长线相交于点
的延长线相交于点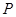 .
.
(1)求证: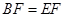 ;
;
(2) 若 , 求
, 求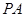 的长.
的长.