(本小题满分12分)在 中,
中, ,
, .
. 求角
求角 的值;
的值; 设
设 ,求
,求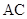 .
.
如图,直线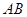 过圆心
过圆心 ,交⊙
,交⊙ 于
于 ,直线
,直线 交⊙
交⊙ 于
于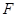 (不与
(不与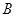 重合),直线
重合),直线 与⊙
与⊙ 相切于
相切于 ,交
,交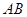 于
于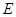 ,且与
,且与 垂直,垂足为
垂直,垂足为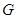 ,连结
,连结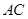 .
.
求证:(1) ;
;
(2)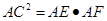 .
.
设函数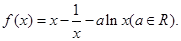
(I)讨论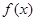 的单调性;
的单调性;
(II)若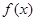 有两个极值点
有两个极值点 和
和 ,记过点
,记过点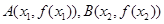 的直线的斜率为
的直线的斜率为 ,问:是否存在
,问:是否存在 ,使得
,使得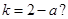 若存在,求出
若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
如图,直角梯形 与等腰直角三角形
与等腰直角三角形 所在的平面互相垂直.
所在的平面互相垂直. ∥
∥ ,
,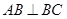 ,
, ,
, .
.
(1)求证: ;
;
(2)求直线 与平面
与平面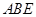 所成角的正弦值;
所成角的正弦值;
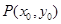
 是双曲线
是双曲线

 上一点,
上一点, 、
、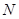 分别是双曲线
分别是双曲线 的左、右顶点,直线
的左、右顶点,直线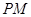 ,
,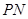 的斜率之积为
的斜率之积为 .
.
(1)求双曲线的离心率;
(2)过双曲线 的右焦点且斜率为1的直线交双曲线于
的右焦点且斜率为1的直线交双曲线于 ,
,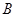 两点,
两点, 为坐标原点,
为坐标原点, 为双曲线上一点,满足
为双曲线上一点,满足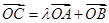 ,求
,求 的值.
的值.
设各项均为正数的等比数列 中,
中, ,
, .设
.设 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,
, ,求证:
,求证: ;
;