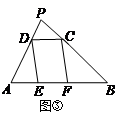如图，在平面直角坐标系中，矩形OCDE的三个顶点分别是C（3，0），D（3，4），E（0，4）．点A在DE上，以A为顶点的抛物线过点C，且对称轴
交z轴于点B．连接EC，AC．点P，Q为动点，设运动时间为t秒．
（1）填空：点A坐标为 ，抛物线的解析式为 ；
（2）在图1中，若点P在线段OC上从点O向点C以1个单位／秒的速度运动，同时，点Q在线段CE上从点C向E以2个单位／秒的速度运动，当一个点到达终点时，另一个点随之停止运动．连接PQ，是否存在实数t，使得PQ所在的直线经过点D，若存在，求出t的值；若不存在，请说明理由；
（3）在图2中，若点P在对称轴上从点A开始向点B以1个单位／秒的速度运动，过点P做PF⊥AB，交AC于点F，过点F作FG⊥AD于点G，交抛物线于点Q，连接AQ，CQ．当t为何值时，△ACQ的面积最大？最大值是多少？
解方程组：
家惠商场服装部为促进营销、吸引顾客，决定试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于45%．试销过程中发现，销售量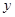
（件）与销售单价
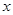（元）之间存在如图所示的一次函数关系．
求
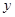关于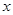的函数关系式（不必写出x的取值范围）；求试销期间该服装部销售该品牌服装获得利润W（元）与销售单价x（元）的函数关系式；销售单价定为多少元时，服装部可获得最大利润，最大利润是多少元？
如果在试销期间该服装部想要获得500元的利润，那么销售单价应定为多少元？
若在试销期间该服装部获得利润不低于500元，试确定销售单价
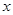的范围．
如图，抛物线y＝ax2＋bx＋c经过原点O，与x轴交于另一点N，直线y＝kx＋4与两坐标轴分别交于A、D两点，与抛物线交于点B(1，m)、C(2，2)．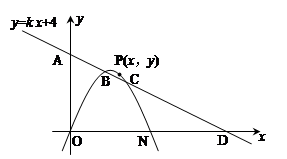
求直线与抛物线的解析式．
若抛物线在x轴上方的部分有一动点P(x，y)，设∠PON＝
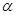，求当△PON的面积最大时tan的值．若动点P保持（2）中的运动线路，问是否存在点P，使得△POA的面积等于△PON的面积的？若存在，请求出点P的坐标；若不存在，请说明理由
在图①至图③中，△ABC为直角三角形，且∠ABC＝90º，∠A＝30º，点P在AC上，∠MPN＝90º．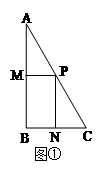
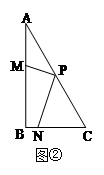
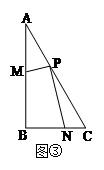
当点P为线段AC的中点，点M、N分别在线段AB、BC上，且PM⊥AB，
PN⊥BC（如图①）时，则PN和PM的数量关系是：PN=________PM；当点P为线段AC的中点，点M、N分别在线段AB、BC上（如图②）时，求
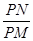的值当PC＝PA，点M、N分别在线段AB、BC上（如图③）时，求
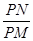的值；
如图①，梯形ABCD中，DC∥AB，DE⊥AB于点E．
阅读理解：
在图①中，延长梯形ABCD的两腰AD、BC交于点P，过点D作DF∥CB交AB于点F，得到图②；四边形BCDF的面积为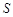
，△ADF的面积
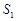，△PDC的面积
．
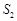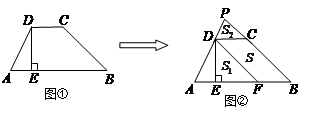
在图②中，若DC=2，AB=8，DE=3，则
，
______，
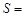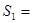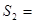；在图②中，若
，
，
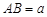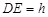，则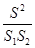
=__________，并写出理由；如图③，□DEFC的四个顶点在△PAB的三边上，若△PDC、△ADE、△CFB的面积分别为2、3、5，试利用（2）中的结论求△PAB的面积．
