选修4-4: 坐标系与参数方程
已知曲线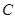 的极坐标方程是
的极坐标方程是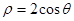 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为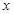 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线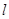 的参数方程是
的参数方程是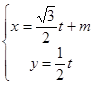 (
(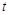 为参数).
为参数).
(Ⅰ)求曲线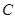 的直角坐标方程和直线
的直角坐标方程和直线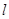 的普通方程;
的普通方程;
(Ⅱ)设点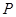
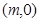 ,若直线
,若直线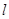 与曲线
与曲线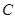 交于
交于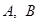 两点,且
两点,且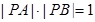 ,求实数
,求实数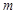 的值.
的值.
点A、B分别是椭圆 长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于
长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于 轴上方,
轴上方, .
.
(1)求点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于 ,求椭圆上的点到点M的距离
,求椭圆上的点到点M的距离 的最小值.
的最小值.
抛物线C的方程为 ,过抛物线C上一点P(x0,y0)(x 0≠0)作斜率为k1,k2的两条直线分别交抛物线C于A(x1,y1)B(x2,y2)两点(P,A,B三点互不相同),且满足
,过抛物线C上一点P(x0,y0)(x 0≠0)作斜率为k1,k2的两条直线分别交抛物线C于A(x1,y1)B(x2,y2)两点(P,A,B三点互不相同),且满足 .
.
(Ⅰ)求抛物线C的焦点坐标和准线方程;
(Ⅱ)设直线AB上一点M,满足 ,证明线段PM的中点在y轴上;
,证明线段PM的中点在y轴上;
(Ⅲ)当 =1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标
=1时,若点P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标 的取值范围.
的取值范围.
如图,圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得 试建立适当的坐标系,并求动点 P的轨迹方程.
试建立适当的坐标系,并求动点 P的轨迹方程.
设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图).现将△ADE沿DE折起,使二面角A-DE-B为45°,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与AE所成角的大小等于_________.
A是椭圆长轴的一个端点,O是椭圆的中心,若椭圆上存在一点P,使∠OPA= ,则椭圆离心率的范围是_________
,则椭圆离心率的范围是_________