(本小题满分7分)选修4-4:坐标系与参数方程
在直角坐标系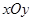 中,直线
中,直线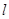 的方程为
的方程为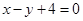 ,曲线
,曲线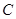 的参数方程
的参数方程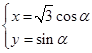 (
(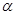 为参数)
为参数)
(I)已知在极坐标系(与直角坐标系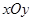 取相同的长度单位,且以原点
取相同的长度单位,且以原点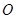 为极点,以
为极点,以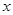 轴正半轴为极轴)中,点
轴正半轴为极轴)中,点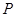 的极坐标
的极坐标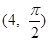 ,判断点
,判断点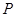 与直线
与直线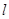 的位置关系;
的位置关系;
(II)设点 为曲线
为曲线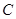 上的一个动点,求它到直线
上的一个动点,求它到直线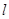 的距离的最小值.
的距离的最小值.
(1)求动点P的轨迹C的方程;
(2)设M、N是直线l上的两个点,点E是点F关于原点的对称点,若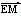 ·
·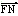 =0,
=0,
求 | MN | 的最小值。
(1)a的值;
(2)函数y=f (x) 的单调区间;
工作,办公室里只有一部电话机,设经该机打进的电话是打给甲、乙、丙的概率依次为 、
、 、
、 。若在一段时间内打进三个电话,且各个电话相互独立。
。若在一段时间内打进三个电话,且各个电话相互独立。
求:(1)这三个电话是打给同一个人的概率。
(2)这三个电话中恰有两个是打给甲的概率。
AD=2,PA=2,PD=2 ,∠PAB=60°。
,∠PAB=60°。
(1)证明:AD⊥平面PAB;
(2)求异面直线PC与AD所成的角的大小;
(3)求二面角P-BD-A的大小。
、已知数列  的前n项和Sn=2n2+2n数列
的前n项和Sn=2n2+2n数列  的前 n 项和 Tn=2-bn
的前 n 项和 Tn=2-bn
(1)求数列  与
与  的通项公式;
的通项公式;
(2)设Cn=an2·bn,证明当且仅当n≥3时,Cn+1<Cn