某市为调研高三一轮复习质量，在2014年10月份组织了一次摸底考试，并从某校2015届高三理科学生在该次考试的数学成绩进行分析，利用分层抽样抽取90分以上的1200名学生的成绩进行分析，已知该样本的容量为20，分数用茎叶图记录如图所示（部分数据丢失），得到的频率分布表如下：
| 分数段 |
 |
 |
 |
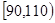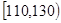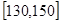| 频数 |
|
|
4 |
| 频率 |
 |
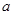0.45 |
0.2 |
(Ⅰ)求表中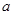的值及分数在
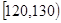范围内的学生人数；
（Ⅱ）从得分在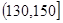
内的学生随机选2名学生的得分，求2名学生的平均分不低于140分的概率.
的圆形村落，A、B两人同时从村落中心出发，B向北直行，A先向东直行，出村后不久，改变前进方向，沿着与村落周界相切的直线前进，后来恰与B相遇.设A、B两人速度一定，其速度比为3：1，问两人在何处相遇？
内有一点
，
为过点
且倾斜角为
的弦，
;
，求点
、
距离的比为
的点的轨迹，则求此曲线的方程.
且到原点的距离等于1的直线方程.
，且与两坐标轴构成周长为10的三角形的直线方程