如图,E、F是四边形ABCD的对角线BD上的两点,AE∥CF,AE=CF,BE=DF.求证:△ADE≌△CBF.
某市计划在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉M到广场的两个入口A、B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A、B、C的位置如图所示,请在原图上利用尺规作图作出音乐喷泉M的位置,(要求:不写已知、求作、作法和结论,保留作图痕迹,必须用铅笔作图)
化简:
如图,在平面直角坐标系xOy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线的对称轴l与x轴相交于点M.
(1)求抛物线对应的函数解析式和对称轴;
(2)设点P为抛物线(x>5)上的一点,若以A、O、M、P为顶点的四边形的四条边的长度为四个连续的正整数,请你直接写出点P的坐标;
(3)连接AC,探索:在直线AC下方的抛物线上是否存在一点N,使△NAC的面积最大?若存在,请你求出点N的坐标;若不存在,请说明理由.
问题:已知方程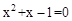 ,求一个一元二次方程,使它的根分别是已知方程根的2倍。
,求一个一元二次方程,使它的根分别是已知方程根的2倍。
解:设所求方程的根为y,则y=2x,所以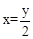
把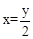 代入已知方程,得
代入已知方程,得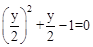
化简,得: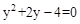
故所求方程为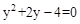
这种利用方程根的代换求新方程的方法,我们称为“换根法”。请阅读材料提供的“换根法”求新方程(要求:把所求方程化成一般形式)
(1)已知方程 ,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为:
,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为:
;
(2)已知关于x的一元二次方程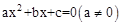 有两个不等于零的实数根,求一个一元二方程,使它的根分别是已知方程的倒数。
有两个不等于零的实数根,求一个一元二方程,使它的根分别是已知方程的倒数。