如图,在平面直角坐标系xOy中,已知抛物线经过点A(0,4),B(1,0),C(5,0),抛物线的对称轴l与x轴相交于点M.
(1)求抛物线对应的函数解析式和对称轴;
(2)设点P为抛物线(x>5)上的一点,若以A、O、M、P为顶点的四边形的四条边的长度为四个连续的正整数,请你直接写出点P的坐标;
(3)连接AC,探索:在直线AC下方的抛物线上是否存在一点N,使△NAC的面积最大?若存在,请你求出点N的坐标;若不存在,请说明理由.
如图,矩形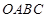 的顶点
的顶点 分别在
分别在 轴和
轴和 轴上,点
轴上,点 的坐标为
的坐标为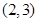 .双曲线
.双曲线 的图像经过
的图像经过 的中点
的中点 ,且与
,且与 交于点
交于点 ,连接
,连接 .
.
(1)求 的值及点
的值及点 的坐标;
的坐标;
(2)若点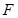 是边上一点,且ΔFCB∽ΔDBE,求直线
是边上一点,且ΔFCB∽ΔDBE,求直线 的解析式
的解析式
某省为解决农村饮用水问题,省财政部门共投资10亿元对各市的农村饮用水的“改水工程”予以一定比例的补助.2012年,A 市在省财政补助的基础上投入600万元用于“改水工程”,计划以后每年以相同的增长率投资,2014年该市计划投资“改水工程”864万元.
(1)求A市投资“改水工程”的年平均增长率;
(2)从2012年到2014年,A市三年共投资“改水工程”多少万元?
先化简,再求值: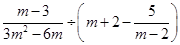 ,其中
,其中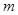 是方程
是方程 的根.
的根.
等边△ABC的边长为6,P为BC边上一点,∠MPN=60°,且PM、PN分别于边AB、AC交于点E、F.
图一图二图三
(1)如图l,当点P为BC的三等分点,且PE⊥AB时,试判断△EPF的形状;
(2)如图2,若点P在BC边上运动,且保持PE⊥AB,设BP= ,四边形AEPF的面积为
,四边形AEPF的面积为 ,求
,求 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;
(3)如图3,若点P在BC边上运动,且MPN绕点P旋转,当CF=AE=2时,求PE的长.
在学习《5.1圆》这一节时,小明遇到了一个问题:如图(1),△ABC与△DBC中,∠A=∠D=90°,M为BC中点,试说明点A、B、C、D在以点M为圆心的同一个圆上.
(1)(2)(3)(4)
小明想到了一个方法,如图(2),连接AM、DM,利用直角三角形的某条性质,得到AM=BM=CM=DM,进而说明了点A、B、C、D在以点M为圆心的同一个圆上.
(1)小明利用的直角三角形的性质是_______________;
(2)在如图(3)的四边形ABDC中,∠A=∠D=90°,点A、B、D、C在同一个圆上吗?说明你的理由.
(3)根据上一问的经验,请解决如下问题:
如图(4),△ABC中,三条高CF、BE、AD相交于点H,连接EF、FD、DE,试说明AD平分∠FDE.