在学习《5．1圆》这一节时，小明遇到了一个问题：如图（1），△ABC与△DBC中，∠A=∠D=90°，M为BC中点，试说明点A、B、C、D在以点M为圆心的同一个圆上．
（1） （2） （3） （4）
小明想到了一个方法，如图（2），连接AM、DM，利用直角三角形的某条性质，得到AM=BM=CM=DM，进而说明了点A、B、C、D在以点M为圆心的同一个圆上．
（1）小明利用的直角三角形的性质是_______________；
（2）在如图（3）的四边形ABDC中，∠A=∠D=90°，点A、B、D、C在同一个圆上吗?说明你的理由．
（3）根据上一问的经验，请解决如下问题：
如图（4），△ABC中，三条高CF、BE、AD相交于点H，连接EF、FD、DE，试说明AD平分∠FDE．
解不等式组：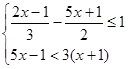
并在数轴上把解集表示出来
因式分解：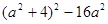
化简：
如图1，在平面直角坐标系中，矩形OABC的顶点O在坐标原点，顶点A、C分别在x轴、y轴的正半轴上，且OA＝2，OC＝1，矩形对角线AC、OB相交于E，过点E的直线与边OA、BC分别相交于点G、H．
(1)①直接写出点E的坐标： ．
②求证：AG＝CH．
(2)如图2，以O为圆心，OC为半径的圆弧交OA与D，若直线GH与弧CD所在的圆相切于矩形内一点F，求直线GH的函数关系式．
(3)在(2)的结论下，梯形ABHG的内部有一点P，当⊙P与HG、GA、AB都相切时，求⊙P的半径．
已知抛物线y＝ax2＋bx＋c经过A(－1，0)、B(3，0)、C(0，3)三点，直线l是抛物线的对称轴．
(1)求抛物线的函数关系式；
(2)设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标；
(3)在直线l上是否存在点M，使△MAC为等腰三角形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．