等边△ABC的边长为6,P为BC边上一点,∠MPN=60°,且PM、PN分别于边AB、AC交于点E、F.
图一 图二 图三
(1)如图l,当点P为BC的三等分点,且PE⊥AB时,试判断△EPF的形状;
(2)如图2,若点P在BC边上运动,且保持PE⊥AB,设BP= ,四边形AEPF的面积为
,四边形AEPF的面积为 ,求
,求 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;
(3)如图3,若点P在BC边上运动,且MPN绕点P旋转,当CF=AE=2时,求PE的长.
已知,E、F是四边形ABCD的对角线AC上的两点,AE=CF,BE=DF,BE∥DF.求证:四边形A BCD是平行四边形.
我市某中学九年级学生对市民“创建精神文明城市“知 晓率采取随机抽样的方法进行问卷调查,问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不太了解“、“从未听说”五个等级,统计后的数据整理如下表:
晓率采取随机抽样的方法进行问卷调查,问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不太了解“、“从未听说”五个等级,统计后的数据整理如下表:
| 等级 |
非常了解 |
比较了解 |
基本了解 |
不太了解 |
从未听说 |
| 频数 |
40 |
60 |
48 |
36 |
16 |
| 频率 |
0.2 |
m |
0.24 |
0.18 |
0.08 |
(1)本次问卷调查抽取的样本容量为 ,表中m的值为 ;
(2)根据表中的数据计算等级为“非常广解”的频数在扇形统计图中所对应扇形的圆心角的度数;
(3)根据上述统计结果,请你对政府相关部门提出一句话建议.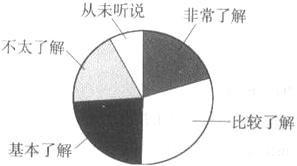
有一个均匀的正六面体,六个面上分别标有数字1,2,3,4,5,6,随机地抛掷一次,把朝上一面的数字记为x;另有三张背面完 全相同,正面分布写有数字﹣2,﹣1,1的卡片,将其混合后,正面朝下放置在桌面上,并从中随机地抽取一张,把卡片正面上的数字记为y;然后计算出S=x+y的值.
全相同,正面分布写有数字﹣2,﹣1,1的卡片,将其混合后,正面朝下放置在桌面上,并从中随机地抽取一张,把卡片正面上的数字记为y;然后计算出S=x+y的值.
(1)用树状图或列表法表示出S的所有可能情况;
(2)求出当S<2时的概率.
解不等式组 .
.
解方程: .
.