(本题满分10分) 如图,在△ABC中,已知AB=AC=5,AD平分∠BAC,E是AC边的中点.
(1)求DE的长;
(2)若AD的长为4,求△DEC的面积.
(1)计算: .
.
(2)先化简,再求值: ,其中
,其中 满足
满足 .
.
已知正比例函数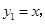 反比例函数
反比例函数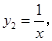 由
由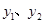 构造一个新函数
构造一个新函数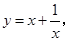 其图象如图所示.(因其图象似双钩,我们称之为“双钩函数” ).给出下列几个命题:
其图象如图所示.(因其图象似双钩,我们称之为“双钩函数” ).给出下列几个命题: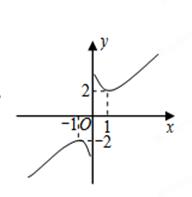
①该函数的图象是中心对称图形;
②当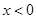 时,该函数在
时,该函数在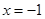 时取得最大值-2;
时取得最大值-2;
③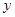 的值不可能为1;
的值不可能为1;
④在每个象限内,函数值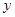 随自变量
随自变量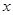 的增大而增大.
的增大而增大.
其中正确的命题是.(请写出所有正确的命题的序号)
如图,已知抛物线y=ax2+bx+c(经过原点)与x轴相交于N点,直线y=kx+4与坐标轴分别相交于A、D两点,与抛物线相交于B(1,m)和C(2,2)两点.
(1)求直线与抛物线的表达式;
(2)求证:C点是△AOD的外心;
(3)若(1)中的抛物线,在x轴上方的部分,有一动点P(x,y),设∠PON=α.当sinα为何值时,△PON的面积有最大值?
(4)若P点保持(3)中运动路线,是否存在△PON,使得其面积等于△OCN面积的 ?若存在,求出动点P的位置;若不存在,请说出理由.
?若存在,求出动点P的位置;若不存在,请说出理由.
如图,矩形ABCD中,P是边AD上的一动点,连接BP、CP,过点B作射线交线段CP的延长线于点E,交AD边于点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x,PM=y.
(1)说明△ABM∽△APB;并求出y关于x的函数关系式,写出自变量x的取值范围;
(2)当AP=4时,求sin∠EBP的值;
(3)如果△EBC是以∠EBC为底角的等腰三角形,求AP的长。
实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=–200x2+400x表示;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y= (k>0)表示(如图所示).
(k>0)表示(如图所示).
(1)喝酒后多长时间血液中的酒精含量达到最大值?最大值为多少?
(2)当 =5时,y=45.求k的值.
=5时,y=45.求k的值.
(3)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.