(本题满分10分) 如图,在△ABC中,点E、G分别在BC、AC上,CD⊥AB,EF⊥AB,垂足分别为D、F.已知∠1+∠2=180°,∠3=105°,求∠ACB的度数.请将求∠ACB度数的过程填写完整.
解:∵EF⊥AB,CD⊥AB,(已知)
∴∠BFE=90°,∠BDC=90°,
理由是: .
∴∠BFE=∠BDC,
∴EF∥CD,理由是: .
∴∠2+∠ =180°,理由是: .
又∵∠1 +∠2=180°(已知),
∴∠1 = .
∴BC∥ ,理由是: .
∴∠3 = ,理由是: .
又∵∠3 = 105°(已知),
∴∠ACB= .
如图,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为80m2?
如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA =∠C.
(1)求证:PB是⊙O的切线;
(2)连接OP,若OP // BC,且OP = 8,⊙O的半径为 ,求BC的长.
,求BC的长.
如图,“和谐号”高铁列车的小桌板收起时近似看作与地面垂直,小桌板的支
架底端与桌面顶端的距离OA = 75厘米.展开小桌板使桌面保持水平,此时CB⊥AO,∠AOB =∠ACB = 37°,
且支架长OB与桌面宽BC的长度之和等于OA的长度.求小桌板桌面的宽度BC.
(参考数据sin37° ≈ 0.6,cos37° ≈ 0.8,tan37° ≈ 0.75)
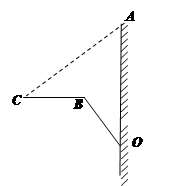
如图,在平面直角坐标系xOy中,⊙A与y轴相切于点B (0,3),与x轴相交于M、N两点.如果点M的坐标为(1,0),求点N的坐标.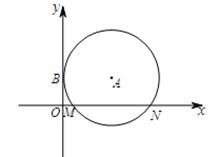
如图,△ABC中,CD是边AB上的高,且 .
.
(1)求证:△ACD∽△CBD;
(2)求∠ACB的大小.