如图，已知∠AOB内部有三条射线，OE平分∠BOC，OF平分∠AOC.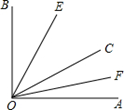
(1)若∠AOB=90°，∠AOC=30°，求∠EOF的度数；
(2)若∠AOB=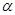
，求∠EOF的度数（写出求解过程）；
(3)若将条件中“OE平分∠BOC，OF平分∠AOC.平分”改为“∠EOB=
∠COB，∠COF=
∠COA”，且∠AOB=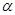，求∠EOF的度数（写出求解过程）.
某公司生产的某种产品每件成本为40元，经市场调查整理出如下信息：①该产品90天内日销售量（m件）与时间（第x天）满足一次函数关系，部分数据如下表：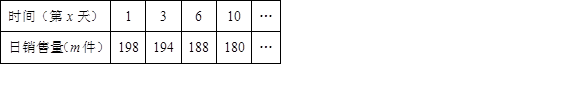
②该产品90天内每天的销售价格与时间（第x天）的关系如下表：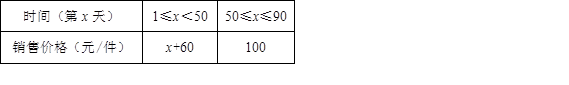
（1）求m关于x的一次函数表达式；
（2）设销售该产品每天利润为y元，请写出y关于x的函数表达式，并求出在90天内该产品哪天的销售利润最大？最大利润是多少？【提示：每天销售利润=日销售量×（每件销售价格﹣每件成本）】
（3）在该产品销售的过程中，共有多少天销售利润不低于5400元，请直接写出结果．
某景点的门票价格如表：
| 购票人数/人 |
1～50 |
51～100 |
100以上 |
| 每人门票价/元 |
12 |
10 |
8 |
某校七年级（1）（2）两班计划去游览该景点，其中（1）班人数少于50人，（2）班人数多于50人且少于100人，如果两班都以班为单位单独购票，则一共支付1118元；如果两班联合起来作为一个团体购票，则只需花费816元．[来@#^源:中教~网*]
（1）两个班各有多少名学生？
（2）团体购票与单独购票相比较，两个班各节约了多少钱？
白溪镇2012年有绿地面积57．5公顷，该镇近几年不断增加绿地面积，2014年达到82．8公顷．
（1）求该镇2012至2014年绿地面积的年平均增长率；
（2）若年增长率保持不变，2015年该镇绿地面积能否达到100公顷？
某地区2013年投入教育经费2500万元，2015年投入教育经费3025万元．
（1）求2013年至2015年该地区投入教育经费的年平均增长率；
（2）根据（1）所得的年平均增长率，预计2016年该地区将投入教育经费多少万元．
某电器商场销售A，B两种型号计算器，两种计算器的进货价格分别为每台30元，40元．商场销售5台A型号和1台B型号计算器，可获利润76元；销售6台A型号和3台B型号计算器，可获利120元．
（1） 求商场销售A，B两种型号计算器的销售价格分别是多少元？（利润=销售价格﹣进货价格）
（2） 商场准备用不多于2500元的资金购进A，B两种型号计算器共70台，问最少需要购进A型号的计算器多少台？