当a>0且x>0时,因为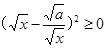 ,所以
,所以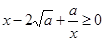 ,从而
,从而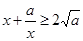 (当x=
(当x=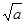 时取等号).记函数
时取等号).记函数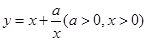 ,由上述结论可知:当x=
,由上述结论可知:当x=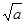 时,该函数有最小值为2
时,该函数有最小值为2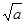
(1)已知函数y1=x(x>0)与函数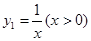 ,则当x= 时,y1+y2取得最小值为
,则当x= 时,y1+y2取得最小值为
(2)已知函数y1=x+1(x>-1)与函数y2=(x+1)2+4(x>−1),求 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值.
如图,光明中学一教学楼顶上竖有一块高为 的宣传牌,点 和点 分别是教学楼底部和外墙上的一点 , , , 在同一直线上),小红同学在距 点9米的 处测得宣传牌底部点 的仰角为 ,同时测得教学楼外墙外点 的仰角为 ,从点 沿坡度为 的斜坡向上走到点 时, 正好与水平线 平行.
(1)求点 到直线 的距离(结果保留根号);
(2)若在点 处测得宣传牌顶部 的仰角为 ,求出宣传牌 的高度(结果精确到 .(注 , , ,

四川省安岳县盛产柠檬和柚子两种水果,今年,某公司计划用两种型号的汽车运输柠檬和柚子到外地销售,运输中要求每辆汽车都要满载满运,且只能装运一种水果.若用3辆汽车装载柠檬、2辆汽车装载柚子可共装载33吨,若用2辆汽车装载柠檬、3辆汽车装载柚子可共装载32吨.
(1)求每辆汽车可装载柠檬或柚子各多少吨?
(2)据调查,全部销售完后,每吨柠檬可获利700元、每吨柚子可获利500元,计划用20辆汽车运输,且柚子不少于30吨,如何安排运输才能使公司获利最大,最大利润是多少元?
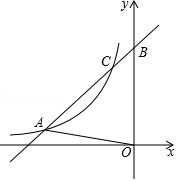
如图,一次函数 的图象与反比例函数 的图象交于点 和点 ,与 轴交于点 , 的面积是6.
(1)求一次函数与反比例函数的解析式;
(2)当 时,比较 与 的大小.
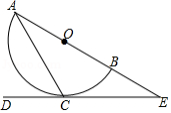
如图, 是半圆的直径, 为弦,过点 作直线 交 的延长线于点 .若 , .
(1)求证:直线 与半圆相切;
(2)若 ,求 的长.
当前, “精准扶贫”工作已进入攻坚阶段, 凡贫困家庭均要“建档立卡” . 某初级中学七年级共有四个班, 已“建档立卡”的贫困家庭的学生人数按一、 二、 三、 四班分别记为 , , , ,现对 , , , 统计后, 制成如图所示的统计图 .
(1) 求七年级已“建档立卡”的贫困家庭的学生总人数;
(2) 将条形统计图补充完整, 并求出 所在扇形的圆心角的度数;
(3) 现从 , 中各选出一人进行座谈, 若 中有一名女生, 中有两名女生, 请用树状图表示所有可能情况, 并求出恰好选出一名男生和一名女生的概率 .
