如图,已知在Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线AB平移至△FEG,DE、FG相交于点H.
(1)判断线段DE、FG的位置关系,并说明理由:
(2)连接CG,求证:四边形CBEG是正方形.(提示:旋转前后,图形中对应的角和对应的边分别相等)
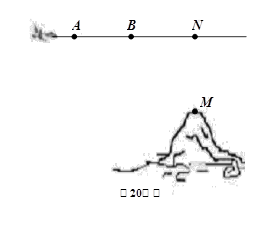
如图,飞机沿水平方向(A、B两点所在直线)飞行,前方有一座高山,为了避免飞机飞行过低,就必须测量山顶M到飞行路线AB的距离MN.飞机能够测量的数据有俯角和飞行距离(因安全因素,飞机不能飞到山顶M的正上方N处才测飞行距离),请你设计一个求距离MN的方案,要求指出需要测量的数据(用字母表示,并在图中标出)
用你所设计测出的数据写出求距离MN的步骤
如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合.连接BE、EC.试猜想线段BE和EC的数量关系和位置关系,并证明你的猜想.
如图,在正方形ABCD中,AB=1,AC是以点B为圆心,AB长为半径的圆的一条弧,点E是边AD上的任意一点(点E与A、D不重合),过E作AC所在圆的切线,交边DC于点F,G为切点当∠DEF=
 时,试说明点G为线段EF的中点;
时,试说明点G为线段EF的中点;设AE=
 ,FC=
,FC= ,用含有
,用含有 的代数式来表示
的代数式来表示 ,并写出
,并写出 的取值范围
的取值范围如果把△DEF沿直线EF对折后得△
 ,如图2,当
,如图2,当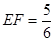 时,讨论△
时,讨论△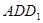 与△
与△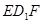 是否相似,如果相似,请加以证明;如果不相似,只要写出结论,不要求写出理由.
是否相似,如果相似,请加以证明;如果不相似,只要写出结论,不要求写出理由.
随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加.据统计,某小区2006年底拥有家庭轿车64辆,2008年底家庭轿车的拥有量达到100辆.若该小区2006年底到2009年底家庭轿车拥有量的年平均增长率都相同,求该小区到2010年底家庭轿车将达到多少辆?
为了缓解停车矛盾,该小区决定投资15万元再建造若干个停车位.据测算,建造费用分别为室内车位5000元/个,露天车位1000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,求该小区最多可建两种车位各多少个?试写出所有可能的方案
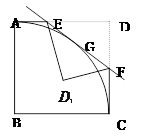
如图, 中,
中, ,以
,以 为直径的
为直径的 交
交 于点
于点 ,过点
,过点 的切线交
的切线交 于
于

求证:

若
 ,求
,求 的长.
的长.