（本小题满分12分）如图，摩天轮上一点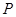
在
时刻距离地面高度满足
，已知某摩天轮的半径为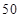
米，点
距地面的高度为
米，摩天轮做匀速转动，每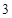
分钟转一圈，点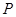的起始位置在摩天轮的最低点处．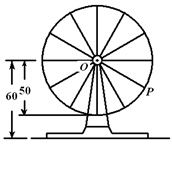
（1）根据条件写出
（米）关于（分钟）的解析式；
（2）在摩天轮转动的一圈内，有多长时间点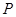距离地面超过
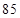米?
已知关于x的实系数二次方程x2+ax+b=0有两个实数根α、β，
证明:|α|<2且|β|<2是2|a|<4+b且|b|<4的充要条件.
已知数列{an}的前n项Sn=pn+q(p≠0,p≠1),求数列{an}是等比数列的充要条件.
已知p:|1－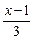
|≤2,q:x2－2x+1－m2≤0(m>0),若⌐p是⌐q的必要而不充分条件，求实数m的取值范围.
如图，已知平行六面体ABCD—A1B1C1D1的底面ABCD是菱形，且∠C1CB=∠C1CD=∠BCD.
(1)求证: C1C⊥BD
(2)当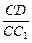
的值为多少时，能使A1C⊥平面C1BD？请给出证明. 
已知函数f1(x)=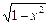
,f2(x)=x+2,
(1)设y=f(x)=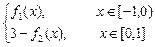
，试画出y=f(x)的图像并求y=f(x)的曲线绕x轴旋转一周所得几何体的表面积；
(2)若方程f1(x+a)=f2(x)有两个不等的实根，求实数a的范围.
(3)若f1(x)>f2(x－b)的解集为［－1，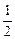
］，求b的值.