如图,已知平行六面体ABCD—A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD.
(1)求证: C1C⊥BD
(2)当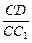 的值为多少时,能使A1C⊥平面C1BD?请给出证明.
的值为多少时,能使A1C⊥平面C1BD?请给出证明. 
已知奇函数 f (x) 在 (-¥,0)∪(0,+¥) 上有意义,且在 (0,+¥) 上是增函数,f (1) = 0,又函数 g(q) = sin 2q+ m cos q-2m,若集合M =" {m" | g(q) < 0},集合 N =" {m" | f [g(q)] < 0},求M∩N.
已知点 是直线
是直线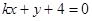
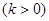 上一动点,
上一动点,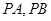 是圆C:
是圆C: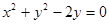 的两条切线,A、B是切点,若四边形
的两条切线,A、B是切点,若四边形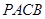 的最小面积是2,则
的最小面积是2,则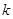 的值为?
的值为?
已知 ,函数
,函数 .
.
(1)求函数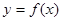 的周期和对称轴方程;
的周期和对称轴方程;
(2)求函数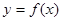 的单调递减区间.
的单调递减区间.
如图,椭圆的中心为原点 ,离心率 ,一条准线的方程是

(Ⅰ)求椭圆的标准方程;
(Ⅱ)设动点
满足:
,其中
、
椭圆上的点,直线
与
的斜率之积为
,
问:是否存在定点
,使得
与点
到直线
:
的距离之比为定值;若存在,求
的坐标,若不存在,说明理由.
如图,在四面体
中,平面
⊥平面
,
,
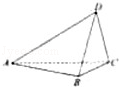
(Ⅰ)求四面体
的体积;
(Ⅱ)求二面角
的平面角的正切值.