已知函数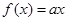 ,
, ,其中
,其中
(Ⅰ)若函数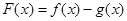 有极值
有极值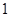 ,求实数
,求实数 的值;
的值;
(Ⅱ)若函数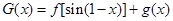 在区间
在区间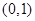 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(Ⅲ)证明: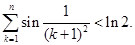
在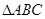 中,内角
中,内角 所对的边分别为
所对的边分别为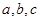 ,且
,且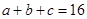
(1)若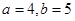 ,求
,求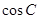 的值;
的值;
(2)若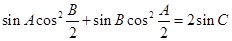 ,且
,且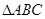 的面积
的面积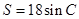 ,求
,求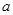 和
和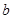 的值.
的值.
对某校高一年级学生参加社区服务次数统计,随机抽去了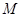 名学生作为样本,得到这
名学生作为样本,得到这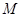 名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表如下:
名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表如下:
(1)求出表中 的值;
的值;
(2)在所取样本中,从参加社区服务的次数不少于 次的学生中任选
次的学生中任选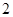 人,求至少一人参加社区服务次数在区间
人,求至少一人参加社区服务次数在区间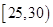 内的概率.
内的概率.
| 分组 |
频数 |
频率 |
 |
9 |
0.45 |
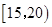 |
5 |
n |
 |
m |
r |
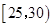 |
2 |
0.1 |
| 合计 |
M |
1 |
已知 ,函数
,函数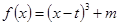 .
.
(1)当 时,若
时,若 ,求函数
,求函数 的单调区间;
的单调区间;
(2)若关于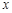 的不等式
的不等式 在区间
在区间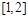 上有解,求
上有解,求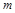 的取值范围;
的取值范围;
(3)已知曲线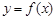 在其图象上的两点
在其图象上的两点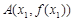 ,
,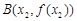 (
(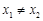 )处的切线分别为
)处的切线分别为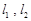 .若直线
.若直线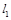 与
与 平行,试探究点
平行,试探究点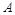 与点
与点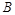 的关系,并证明你的结论.
的关系,并证明你的结论.
已知抛物线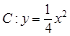 的焦点为
的焦点为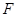 ,点
,点 为抛物线
为抛物线 上的一个动点,过点
上的一个动点,过点 且与抛物线
且与抛物线 相切的直线记为
相切的直线记为 .
.
(1)求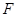 的坐标;
的坐标;
(2)当点 在何处时,点
在何处时,点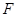 到直线
到直线 的距离最小?
的距离最小?
已知: 为常数)
为常数)
(1)若 ,求
,求 的最小正周期;
的最小正周期;
(2)若 在[
在[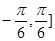 上最大值与最小值之和为3,求
上最大值与最小值之和为3,求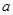 的值.
的值.