（本小题满分12分）某学校举行元旦晚会，组委会招募了12名男志愿者和18名 女志愿者，将这30名志愿者的身高编成如图所示的茎叶图（单位：cm），身高在175 cm以上（包括175 cm）定义为“高个子”，身高在175 cm以下（不包括175 cm）定义为“非高个子”．
（1）如果用分层抽样的方法从“高个子”和“非高个子”中共抽取5人，再从这5人中选2人，求至少有一人是“高个子”的概率；
（2）若从身高180 cm以上（包括180 cm）的志愿者中选出男、女各一人，求这2人身高相差5 cm以上的概率．
在四边形ABCD中，对角线AC、BD交于点O且|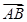
|＝|
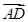|＝1，
＋
＝
＋
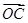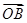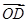＝0，cos∠DAB＝
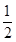.求|
＋
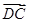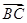|与|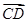
＋|.
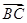在水流速度大小为10km/h的河中，如果要使船实际以10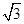
km/h大小的速度与河岸成直角横渡，求船行驶速度的大小与方向．
已知两个力F1、F2的方向互相垂直，且它们的合力F大小为10N，与力F1的夹角是60°，求力F1、F2的大小．
设a表示“向西走2km”，b表示“向北走2km”，则a＋b表示向哪个方向行走了多少？
已知函数f(x)＝Acos(ωx＋φ)＋b(A>0，ω>0，|φ|<
)在同一个周期内的图象上有一个最大值点A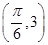
和一个最小值点B
.
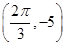(1)求f(x)的解析式；
(2)经过怎样的平移和伸缩变换可以将f(x)的图象变换为g(x)＝cosx的图象．