某市为了了解本市高中学生的汉字书写水平，在全市范围内随机抽取了近千名学生参加汉字听写考试，将所得数据整理后，绘制出频率分布直方图如图所示，其中样本数据分组区间为
，
，
，
，
．
（1）试估计全市学生参加汉字听写考试的平均成绩；
（2）如果从参加本次考试的同学中随机选取1名同学，求这名同学考试成绩在80分以上（含80分）的概率；
（3）如果从参加本次考试的同学中随机选取3名同学，这3名同学中考试成绩在80分以上（含80分）的人数记为
，求的分布列及数学期望．
（注：频率可以视为相应的概率）
已知抛物线E:y2= 4x，点P（2，O）．如图所示，直线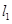
．过点P且与抛物线E交于A（xl，y1）、B（ x2，y2）两点，直线
过点P且与抛物线E交于C（x3， y3）、D（x4，y4）两点．过点P作x轴的垂线，与线段AC和BD分别交于点M、N．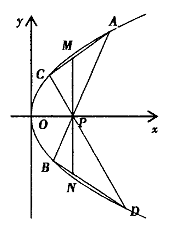
（I）求y1y2的值；
（Ⅱ）求讧：|PM|="|" PN|
几何体EFG —ABCD的面ABCD，ADGE，DCFG均为矩形，AD=DC=l，AE=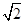
。
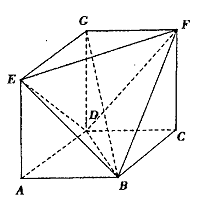
（I）求证：EF⊥平面GDB；
（Ⅱ）线段DG上是否存在点M使直线BM与平面BEF所成的角为45°，若存在求等￥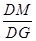
的值；若不存在，说明理由．
甲乙两班进行消防安全知识竞赛，每班出3人组成甲乙两支代表队，首轮比赛每人一道必答题，答对则为本队得1分，答错不答都得0分，已知甲队3人每人答对的概率分别为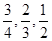
，乙队每人答对的概率都是
．设每人回答正确与否相互之间没有影响，用
表示甲队总得分．
（I）求随机变量的分布列及其数学期望E（）；
（Ⅱ）求在甲队和乙队得分之和为4的条件下，甲队比乙队得分高的概率．
在△ABC中角，A，B，C所对的边分别为a,b,c，向量m=（cos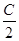
，1），n=（一l,sin（A+B）），且m⊥n．
（ I）求角C的大小；
（Ⅱ）若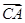
·
，且a+b =4，求c．
已知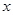
满足不等式
，求函数
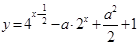的最小值．