如图,在平面直角坐标系 中,离心率为
中,离心率为 的椭圆
的椭圆
 的左顶点为
的左顶点为 ,过原点
,过原点 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆 交于
交于 两点,直线
两点,直线 分别与
分别与 轴交于
轴交于 两点.若直线
两点.若直线 斜率为
斜率为 时,
时, .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)试问以 为直径的圆是否经过定点(与直线
为直径的圆是否经过定点(与直线 的斜率无关)?请证明你的结论.
的斜率无关)?请证明你的结论.
【2015高考山东,理20】平面直角坐标系 中,已知椭圆
中,已知椭圆 的离心率为
的离心率为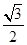 ,左、右焦点分别是
,左、右焦点分别是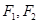 ,以
,以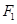 为圆心以3为半径的圆与以
为圆心以3为半径的圆与以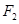 为圆心以1为半径的圆相交,且交点在椭圆
为圆心以1为半径的圆相交,且交点在椭圆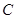 上.
上.
(Ⅰ)求椭圆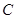 的方程;
的方程;
(Ⅱ)设椭圆 ,
,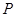 为椭圆
为椭圆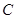 上任意一点,过点
上任意一点,过点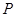 的直线
的直线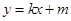 交椭圆
交椭圆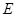 于
于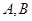 两点,射线
两点,射线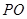 交椭圆
交椭圆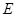 于点
于点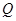 .
.
(ⅰ)求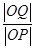 的值;
的值;
(ⅱ)求 面积的最大值.
面积的最大值.
【2015高考浙江,理19】已知椭圆 上两个不同的点
上两个不同的点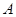 ,
,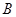 关于直线
关于直线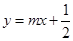 对称.
对称.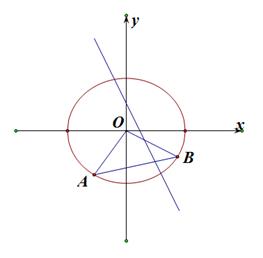
(1)求实数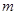 的取值范围;
的取值范围;
(2)求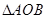 面积的最大值(
面积的最大值(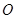 为坐标原点).
为坐标原点).
【2015高考福建,理18】已知椭圆E: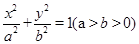 过点
过点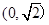 ,且离心率为
,且离心率为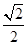 .
.
(Ⅰ)求椭圆E的方程;
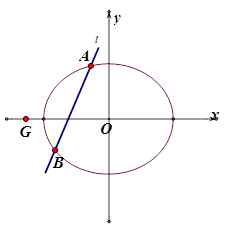
(Ⅱ)设直线 交椭圆E于A,B两点,判断点G
交椭圆E于A,B两点,判断点G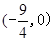 与以线段AB为直径的圆的位置关系,并说明理由.
与以线段AB为直径的圆的位置关系,并说明理由.
【2015江苏高考,18】(本小题满分16分)如图,在平面直角坐标系xOy中,已知椭圆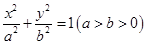 的离心率为
的离心率为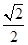 ,且右焦点F到左准线l的距离为3.
,且右焦点F到左准线l的距离为3.
(1)求椭圆的标准方程;
(2)过F的直线与椭圆交于A,B两点,线段AB的垂直平分线分别交直线l和AB于点P,C,若PC=2AB,求直线AB的方程.
【2015高考新课标2,理20】已知椭圆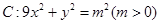 ,直线
,直线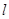 不过原点
不过原点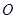 且不平行于坐标轴,
且不平行于坐标轴,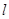 与
与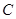 有两个交点
有两个交点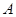 ,
,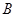 ,线段
,线段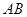 的中点为
的中点为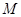 .
.
(Ⅰ)证明:直线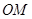 的斜率与
的斜率与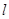 的斜率的乘积为定值;
的斜率的乘积为定值;
(Ⅱ)若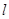 过点
过点 ,延长线段
,延长线段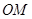 与
与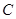 交于点
交于点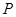 ,四边形
,四边形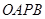 能否为平行四边形?若能,求此时
能否为平行四边形?若能,求此时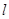 的斜率,若不能,说明理由.
的斜率,若不能,说明理由.