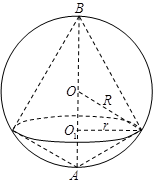
一个透明的球形装饰品内放置了两个公共底面的圆锥，且这两个圆锥的顶点和底面圆周都在这个球面上，如图，已知圆锥底面面积是这个球面面积的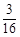
，设球的半径为
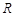，圆锥底面半径为
.
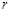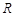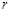（1）试确定与的关系，并求出较大圆锥与较小圆锥的体积之比；
（2）求出两个圆锥的体积之和与球的体积之比.
（本小题满分13分）已知函数
.
(1）若函数
在
上单调递增，求实数
的取值范围.
(2）记函数
，若
的最小值是
，求函数的解析式.
（本小题满分12分）已知椭圆方程为
斜率为
的直线过椭圆的上焦点且与椭圆相交于P，Q两点，线段PQ的垂直平分线与y轴交于点M(0，m)。
（1）求m的取值范围；
（2）求△OPQ面积的取值范围。
（本小题满分12分）如图，四棱锥P-ABCD中底面ABCD为矩形，PD⊥底面ABCD，AD=PD=1，AB=
BC，E、F分别为CD、PB的中点。
（1）求证：EF⊥平面PAB；
（2）求三棱锥P-AEF的体积
（本小题满分12分）一个袋中装有四个形状大小完全相同的球，球的编号分别为1，2，3，4．
（1）从袋中随机抽取一个球，将其编号记为
，然后从袋中余下的三个球中再随机抽取一个球，将其编号记为
．求关于
的一元二次方程
有实根的概率；
（2）先从袋中随机取一个球，该球的编号为
，将球放回袋中，然后再从袋中随机取一个球，该球的编号为
．若以
作为点P的坐标，求点P落在区域
内的概率．
（本小题满分12分）设数列
的前
项和为
，已知
（1）求数列的通项公式；
（2）若
，求数列
的前项和