已知函数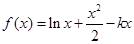 ,其中常数
,其中常数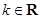 .
.
(1)求 的单调增区间与单调减区间;
的单调增区间与单调减区间;
(2)若 存在极值且有唯一零点
存在极值且有唯一零点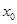 ,求
,求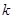 的取值范围及不超过
的取值范围及不超过 的最大整数
的最大整数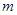 .
.
(本小题满分13分)已知抛物线 ,直线
,直线 截抛物线C所得弦长为
截抛物线C所得弦长为 .
.
(1)求抛物线的方程;
(2)已知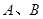 是抛物线上异于原点
是抛物线上异于原点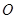 的两个动点,记
的两个动点,记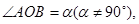 若
若 试求当
试求当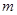 取得最小值时
取得最小值时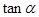 的最大值;
的最大值;
(3)设抛物线的内接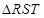 的重心为焦点F,试探求
的重心为焦点F,试探求 是否为定值?若是,求出该定值,若不是,请说明理由.
是否为定值?若是,求出该定值,若不是,请说明理由.
(本小题满分12分)已知等比数列 的首项
的首项 ,公比
,公比 ,数列
,数列 前
前 项的积记为
项的积记为 .
.
(1)求使得 取得最大值时
取得最大值时 的值;
的值;
(2)证明 中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这些等差数列的公差按从小到大的顺序依次设为
中的任意相邻三项按从小到大排列,总可以使其成等差数列,如果所有这些等差数列的公差按从小到大的顺序依次设为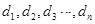 ,求数列
,求数列 的通项公式.
的通项公式.
(参考数据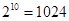 )
)
(本小题满分12分)如图是三棱柱 的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,
的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形, 为
为 的中点.
的中点.
(1)求证: ∥平面
∥平面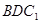 ;
;
(2)设 垂直于
垂直于 ,求二面角
,求二面角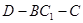 的大小.
的大小.
(本小题满分12分)已知正方形 的边长为2,
的边长为2, 分别是边
分别是边 的中点.
的中点.
(1)在正方形 内部随机取一点
内部随机取一点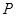 ,求满足
,求满足 的概率;
的概率;
(2)从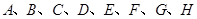 这八个点中,随机选取两个点,记这两个点之间的距离的平方为
这八个点中,随机选取两个点,记这两个点之间的距离的平方为 ,求随机变量
,求随机变量 的分布列与数学期望
的分布列与数学期望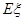 .
.
(本小题满分12分)已知函数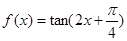 .
.
(1)求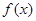 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(2)设 ,若
,若 求
求 的大小.
的大小.