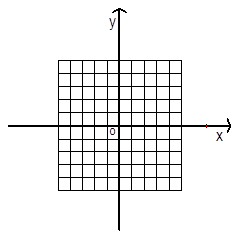（本小题满分12分） 如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=3cm．动点M从点C出发，以每秒1cm的速度沿CA向终点A移动，同时动点P从点A出发，以每秒2cm的速度沿AB向终点B移动，连接PM，设移动时间为t（s）（0＜t＜2.5）．
（1）当AP=AM时，求t的值.
（2）设四边形BPMC的面积为
（cm²），求y与t之间的函数关系式；
（3）是否存在某一时刻t，使四边形BPMC的面积是Rt△ABC面积的
？若存在，求出相应t的值，若不存在，说明理由；
（4）是否存在某一时刻t，使以M，P，A为顶点的三角形与△ABC相似？若存在，求出相应t的值;若不存在，说明理由.
化简（4分×4，共16分）（1）2x2y－2xy－4xy2＋xy＋4x2y－3xy2
(2) 3 (4x2－3x＋2)－2 (1－4x2＋x)
（3）5abc－2a2b－[ 3abc－3 (4ab2+a2b)]
(4) （2x2＋x）－2［x2－2（3 x2－x）］
如图(1)，在⊿ABC中，AE=EB,AF=FC,则EF与BC存在以下关系：EF∥BC,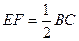 
;将AC沿BC方向平移到DH，得图(2)，沿CB方向平移到DH得图(3)，图(2)中AD与BH存在关系：EF∥AD, 
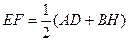;，那么在图(3)中是否有类似于图(1)(2)中的结论，请把猜想的结论填在方框内，并就图(3)的结论加以证明。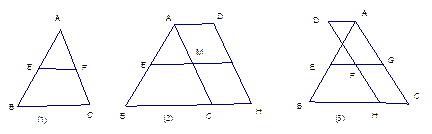
某工程队在我县实施一江两岸山水园林县城的改造建设中，承包了一项拆迁工程，原计划每天拆1250m2，因为准备工作不足，第一天少拆20%，从第二天开始，该工程队加快拆迁速度，第三天就拆迁了1440m2，
问：该工程队第一天拆迁面积是多少？
若该工程队第二、三天拆迁面积比前一天增加的百分数相同，求这个百分数。
为了测量学校操场上旗杆的高度，小明请同学帮忙，测量了同一时刻自己的影长EC和旗杆的影长BC分别为0.6m和3.6m，如图，如果小身高CD为1.5m，请计算旗杆AB的高度。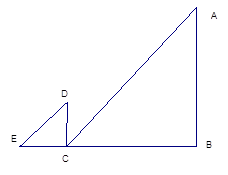
如图，⊿ABC在平面直角坐标系内三顶点坐标分别为
先画出⊿ABC；
以B为位似中心，画出⊿A1B1C1，使⊿A1B1C1与⊿ABC相似且相似比为2:1
