(本小题满分14分)如图,在边长为 的菱形
的菱形 中,
中, ,点
,点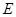 ,
,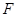 分别是边
分别是边 ,
,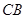 的中点,
的中点,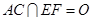 ,沿
,沿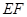 将△
将△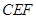 翻折到△
翻折到△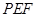 ,连接
,连接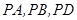 ,得到如图的五棱锥
,得到如图的五棱锥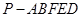 ,且
,且 .
.
(1)求证: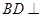 平面
平面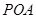 ;
;
(2)求二面角 的正切值.
的正切值.
已知数列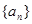 的首项为
的首项为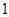 ,对任意的
,对任意的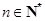 ,定义
,定义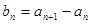 .
.
(Ⅰ) 若 ,
,
(i)求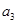 的值和数列
的值和数列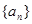 的通项公式;
的通项公式;
(ii)求数列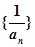 的前
的前 项和
项和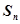 ;
;
(Ⅱ)若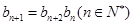 ,且
,且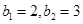 ,求数列
,求数列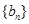 的前
的前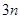 项的和.
项的和.
已知在四棱锥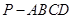 中,
中,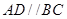 ,
,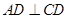 ,
,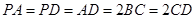 ,
,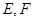 分别是
分别是 的中点.
的中点.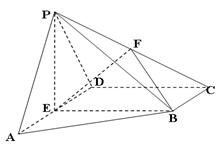
(Ⅰ)求证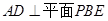 ;
;
(Ⅱ)求证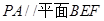 ;
;
(Ⅲ)若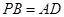 ,求二面角
,求二面角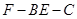 的大小.
的大小.
已知函数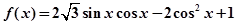
(Ⅰ)求函数 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(Ⅱ)在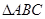 中,若
中,若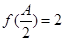 ,
,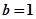 ,
, ,求
,求 的值.
的值.
某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六组: ,
,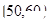 ,…,
,…,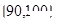 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.
(Ⅰ)求图中实数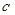 的值;
的值;
(Ⅱ)若该校高一年级共有学生500人,试估计该校高一年级在这次考试中成绩不低于60分的人数;
(Ⅲ)若从样本中数学成绩在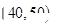 与
与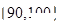 两个分数段内的学生中随机选取两名学生,试用列举
两个分数段内的学生中随机选取两名学生,试用列举
法求这两名学生的数学成绩之差的绝对值不大于10的概率.
在数列{an}(n∈N*)中,已知a1=1,a2k=-ak,a2k-1=(-1)k+1ak,k∈N*. 记数列{an}的前n项和为Sn.
(1)求S5,S7的值;
(2)求证:对任意n∈N*,Sn≥0.