某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六组: ,
,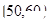 ,…,
,…,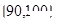 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.
(Ⅰ)求图中实数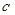 的值;
的值;
(Ⅱ)若该校高一年级共有学生500人,试估计该校高一年级在这次考试中成绩不低于60分的人数;
(Ⅲ)若从样本中数学成绩在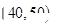 与
与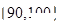 两个分数段内的学生中随机选取两名学生,试用列举
两个分数段内的学生中随机选取两名学生,试用列举
法求这两名学生的数学成绩之差的绝对值不大于10的概率.
(本小题共13分)已知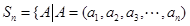 ,
,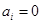 或1,
或1,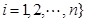
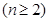 ,对于
,对于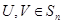 ,
,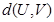 表示U和V中相对应的元素不同的个数.
表示U和V中相对应的元素不同的个数.
(Ⅰ)令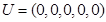 ,存在m个
,存在m个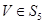 ,使得
,使得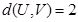 ,写出m的值;
,写出m的值;
(Ⅱ)令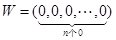 ,若
,若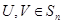 ,求证:
,求证: ;
;
(Ⅲ)令 ,若
,若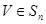 ,求所有
,求所有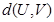 之和.
之和.
(本小题共14分) 已知点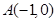 ,
,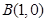 ,动点P满足
,动点P满足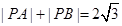 ,记动点P的轨迹为W.
,记动点P的轨迹为W.
(Ⅰ)求W的方程;
(Ⅱ)直线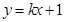 与曲线W交于不同的两点C,D,若存在点
与曲线W交于不同的两点C,D,若存在点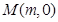 ,使得
,使得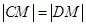 成立,求实数m的取值范围.
成立,求实数m的取值范围.
(本小题共13分)已知函数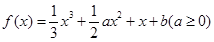 ,
,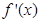 为函数
为函数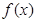 的导函数.
的导函数.
(Ⅰ)设函数f(x)的图象与x轴交点为A,曲线y=f(x)在A点处的切线方程是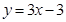 ,求
,求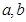 的值;
的值;
(Ⅱ)若函数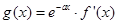 ,求函数
,求函数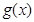 的单调区间.
的单调区间.
(本小题共13分)某商场在店庆日进行抽奖促销活动,当日在该店消费的顾客可参加抽奖.抽奖箱中有大小完全相同的4个小球,分别标有字“生”“意”“兴”“隆”.顾客从中任意取出1个球,记下上面的字后放回箱中,再从中任取1个球,重复以上操作,最多取4次,并规定若取出“隆”字球,则停止取球.获奖规则如下:依次取到标有“生”“意”“兴”“隆”字的球为一等奖;不分顺序取到标有“生”“意”“兴”“隆”字的球,为二等奖;取到的4个球中有标有“生”“意”“兴”三个字的球为三等奖.
(Ⅰ)求分别获得一、二、三等奖的概率;
(Ⅱ)设摸球次数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(本小题共14分)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD//BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=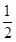 AD=1,CD=
AD=1,CD= .
.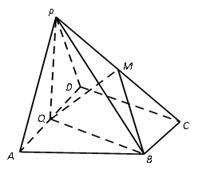
(Ⅰ)若点M是棱PC的中点,求证:PA // 平面BMQ;
(Ⅱ)求证:平面PQB⊥平面PAD;
(Ⅲ)若二面角M-BQ-C为30°,设PM=tMC,试确定t的值 .