对于定义域为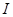 的函数
的函数 ,如果存在区间
,如果存在区间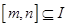 ,同时满足:
,同时满足:
① 在
在 内是单调函数;②当定义域是
内是单调函数;②当定义域是 ,
, 值域也是
值域也是 ,则称
,则称 是函数
是函数
的“好区间”.
(1)设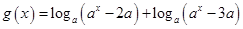 (其中
(其中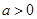 且
且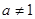 ),判断
),判断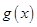 是否存在“好区间”,并
是否存在“好区间”,并
说明理由;
(2)已知函数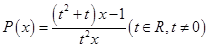 有“好区间”
有“好区间” ,当
,当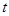 变化时,求
变化时,求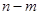 的最大值.
的最大值.
(本小题满分16分)对于给定数列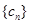 ,如果存在实常数
,如果存在实常数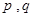 使得
使得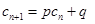 对于任意
对于任意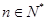 都成立,我们称数列
都成立,我们称数列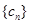 是 “线性数列”.
是 “线性数列”.
(1)若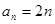 ,
,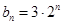 ,
,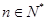 ,数列
,数列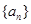 、
、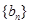 是否为“线性数列”?若是,指出它对应的实常数
是否为“线性数列”?若是,指出它对应的实常数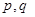 ,若不是,请说明理由;
,若不是,请说明理由;
(2)证明:若数列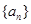 是“线性数列”,则数列
是“线性数列”,则数列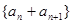 也是“线性数列”;
也是“线性数列”;
(3)若数列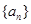 满足
满足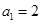 ,
,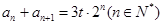 ,
,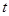 为常数.求数列
为常数.求数列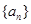 前
前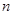 项的和.
项的和.
(本小题满分16分)已知A(-2,0),B(2,0)为椭圆C的左、右顶点,F为其右焦点,P是椭圆C上异于A,B的动点,且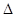 APB面积的最大值为2
APB面积的最大值为2 .
.
(1)求椭圆C的方程及离心率;
(2)直线AP与椭圆在点B处的切线交于点D,当直线AP绕点A转动时,试判断以BD为直径的圆与直线PF的位置关系,并加以证明.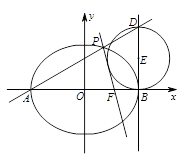
(本小题满分14分)某市近郊有一块大约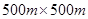 的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米.
的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米.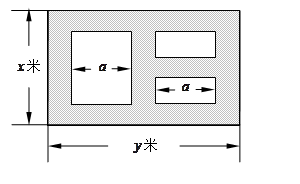
(1)分别用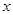 表示
表示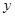 和S的函数关系式,并给出定义域;
和S的函数关系式,并给出定义域;
(2)怎样设计能使S取得最大值,并求出最大值.
(本小题满分14分)如图,已知斜三棱柱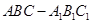 中,
中,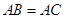 ,
, 为
为 的中点.
的中点.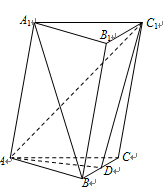
(1)若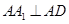 ,求证:
,求证: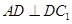 ;
;
(2)求证: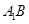 ∥平面
∥平面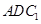 .
.
(本小题满分14分)在△ABC中,内角A,B,C的对边分别为a,b,c,若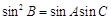 .
.
(1)求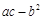 的值;
的值;
(2)若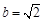 ,且
,且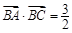 ,求
,求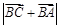 的值.
的值.