(本小题满分14分)如图,已知斜三棱柱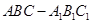 中,
中,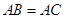 ,
, 为
为 的中点.
的中点.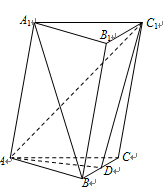
(1)若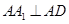 ,求证:
,求证: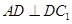 ;
;
(2)求证: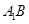 ∥平面
∥平面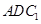 .
.
已知函数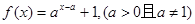 恒过定点
恒过定点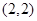 .
.
(1)求实数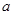 ;
;
(2)在(1)的条件下,将函数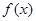 的图象向下平移1个单位,再向左平移
的图象向下平移1个单位,再向左平移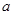 个单位后得到函数
个单位后得到函数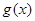 ,设函数
,设函数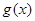 的反函数为
的反函数为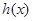 ,求
,求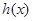 的解析式;
的解析式;
(3)对于定义在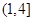 上的函数
上的函数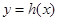 ,若在其定义域内,不等式
,若在其定义域内,不等式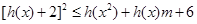 恒成立,求
恒成立,求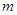 的取值范围.
的取值范围.
已知二次函数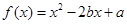 ,满足
,满足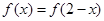 ,且方程
,且方程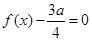 有两个相等的实根.
有两个相等的实根.
(1)求函数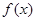 的解析式;
的解析式;
(2)当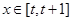
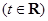 时,求函数
时,求函数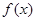 的最小值
的最小值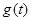 的表达式.
的表达式.
已知函数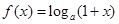 ,
,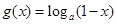 ,其中
,其中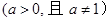 ,设
,设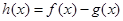 .
.
(1)求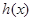 的定义域;
的定义域;
(2)判断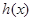 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(3)若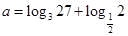 ,求使
,求使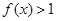 成立的
成立的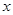 的集合.
的集合.
石家庄市为鼓励居民节约用电,采用分段计费的方法计算电费,每月用电不超过100度时,按每度0.52元计算,每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.6元计算.
(1)设月用电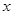 度时,应缴电费
度时,应缴电费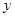 元,写出
元,写出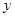 关于
关于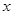 的函数关系式;
的函数关系式;
(2)小明家第一季度缴纳电费情况如下:
| 月份 |
一月 |
二月 |
三月 |
合计 |
| 缴费金额 |
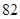 元 元 |
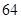 元 元 |
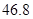 元 元 |
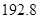 元 元 |
问小明家第一季度共用电多少度?
设集合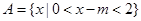 ,
,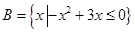 ,分别求满足下列条件的实数
,分别求满足下列条件的实数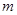 的取值范围:(1)
的取值范围:(1)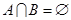 ;(2)
;(2)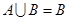 .
.