(本小题满分16分)已知A(-2,0),B(2,0)为椭圆C的左、右顶点,F为其右焦点,P是椭圆C上异于A,B的动点,且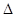 APB面积的最大值为2
APB面积的最大值为2 .
.
(1)求椭圆C的方程及离心率;
(2)直线AP与椭圆在点B处的切线交于点D,当直线AP绕点A转动时,试判断以BD为直径的圆与直线PF的位置关系,并加以证明.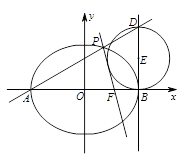
已知圆C的半径为2,圆心在x轴的正半轴上,直线 与圆C相切.
与圆C相切.
(I)求圆C的方程;
(II)过点Q(0,-3)的直线 与圆C交于不同的两点A
与圆C交于不同的两点A 、B
、B ,当
,当 时,求△AOB的面积.
时,求△AOB的面积.
.(12分)如图,在四棱台ABCD-A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2.
(1)求证:B1B∥平面D1AC;
(2)求证:平面D1AC⊥平面B1BDD1.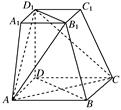
(1)已知 是奇函数,求常数
是奇函数,求常数 的值;
的值;
(2)画出函数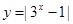 的图象,并利用图象回答:
的图象,并利用图象回答: 为何值时,方程|
为何值时,方程| |=
|= 无解?有一解?有两解?
无解?有一解?有两解?
.已知△ABC的三个顶点分别为A(2,3),B(-1,-2),C(-3,4),求
(1)BC边上的中线AD所在的直线方程;
(2)△ABC的面积。
求与圆 外切且与直线
外切且与直线 相切于点
相切于点 的圆的方程.
的圆的方程.