(本小题满分14分)某市近郊有一块大约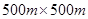 的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米.
的接近正方形的荒地,地方政府准备在此建一个综合性休闲广场,首先要建设如图所示的一个矩形场地,其中总面积为3000平方米,其中阴影部分为通道,通道宽度为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S平方米.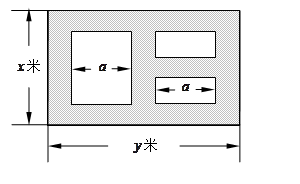
(1)分别用 表示
表示 和S的函数关系式,并给出定义域;
和S的函数关系式,并给出定义域;
(2)怎样设计能使S取得最大值,并求出最大值.
如图,菱形 的边长为4,
的边长为4, ,
, .将菱形
.将菱形 沿对角线
沿对角线 折起,得到三棱锥
折起,得到三棱锥 ,点
,点 是棱
是棱 的中点,
的中点, .
.
(1)求证: 平面
平面 ;
;
(2)求证:平面
 平面
平面 ;
;
(3)求三棱锥 的体积.
的体积.
为了对某课题进行研究,用分层抽样方法从三所科研单位A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人):
| 科研单位 |
相关人数 |
抽取人数 |
| A |
16 |
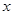 |
| B |
12 |
3 |
| C |
8 |
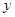 |
(1)确定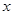 与
与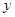 的值;
的值;
(2)若从科研单位A、C抽取的人中选2人作专题发言,求这2人都来自科研单位A的概率.
已知函数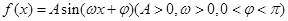 ,
,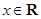 的最大值是1,最小正周期是
的最大值是1,最小正周期是 ,其图像经过点
,其图像经过点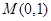 .
.
(1)求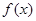 的解析式;
的解析式;
(2)设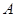 、
、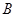 、
、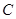 为△ABC的三个内角,且
为△ABC的三个内角,且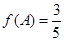 ,
,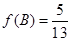 ,求
,求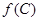 的值.
的值.
已知函数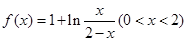 .
.
(1)是否存在点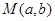 ,使得函数
,使得函数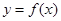 的图像上任意一点P关于点M对称的点Q也在函数
的图像上任意一点P关于点M对称的点Q也在函数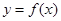 的图像上?若存在,求出点M的坐标;若不存在,请说明理由;
的图像上?若存在,求出点M的坐标;若不存在,请说明理由;
(2)定义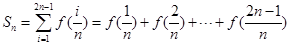 ,其中
,其中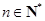 ,求
,求 ;
;
(3)在(2)的条件下,令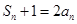 ,若不等式
,若不等式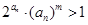 对
对 且
且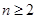 恒成立,求实数
恒成立,求实数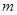 的取值范围.
的取值范围.
已知椭圆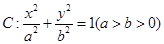 的左、右焦点分别为
的左、右焦点分别为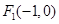 、
、 ,P为椭圆
,P为椭圆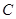 上任意一点,且
上任意一点,且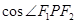 的最小值为
的最小值为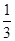 .
.
(1)求椭圆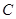 的方程;
的方程;
(2)动圆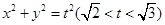 与椭圆
与椭圆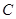 相交于A、B、C、D四点,当
相交于A、B、C、D四点,当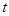 为何值时,矩形ABCD的面积取得最大值?并求出其最大面积.
为何值时,矩形ABCD的面积取得最大值?并求出其最大面积.