已知数列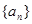 的首项为
的首项为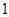 ,对任意的
,对任意的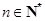 ,定义
,定义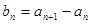 .
.
(Ⅰ) 若 ,
,
(i)求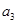 的值和数列
的值和数列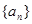 的通项公式;
的通项公式;
(ii)求数列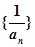 的前
的前 项和
项和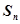 ;
;
(Ⅱ)若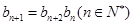 ,且
,且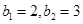 ,求数列
,求数列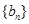 的前
的前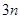 项的和.
项的和.
(Ⅰ)求证:数列{xn}是等比数列;
(Ⅱ)设 满足
满足
ys=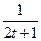 ,yt=
,yt= (s,t∈N,且s≠t)共中a为常数,且1<a<
(s,t∈N,且s≠t)共中a为常数,且1<a< ,试判断,是否存在自然
,试判断,是否存在自然
数M,使当n>M时,xn>1恒成立?若存在,求出相应的M;若不存在,请说明理由




 为
为 上的点,且
上的点,且 ,
, .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求三棱锥 的体积
的体积
已知函数 .
.
(1)若点
 (
( )为函数
)为函数 与
与 的图象的公共点,试求实数
的图象的公共点,试求实数 的值;
的值;
(2)设 是函数
是函数 的图象的一条对称轴,求
的图象的一条对称轴,求 的值;
的值;
(3)求函数 的值域
的值域
已知函数y="f(x)="  (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)< 
(1)试求函数f(x)的解析式;
(2)问函数f(x)图象上是否存在关于点(1,0)对称的两点,若存在,求出点的坐标;若不存在,说明理由。
设 的定义域
的定义域 ,对于任意正实数m,n恒有
,对于任意正实数m,n恒有 ,且当
,且当 时,
时, .
.
(1)求 的值;(2)求证:
的值;(2)求证: 在
在 上是增函数;
上是增函数;
(3)解关于x的不等式 ,其中
,其中 .
.