(Ⅰ)求证:数列{xn}是等比数列;
(Ⅱ)设 满足
满足
ys=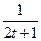 ,yt=
,yt= (s,t∈N,且s≠t)共中a为常数,且1<a<
(s,t∈N,且s≠t)共中a为常数,且1<a< ,试判断,是否存在自然
,试判断,是否存在自然
数M,使当n>M时,xn>1恒成立?若存在,求出相应的M;若不存在,请说明理由
已知函数 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)当 时,求函数
时,求函数 的最大值和最小值.
的最大值和最小值.
在无穷数列 中,
中, ,对于任意
,对于任意 ,都有
,都有 ,
,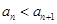 . 设
. 设 , 记使得
, 记使得 成立的
成立的 的最大值为
的最大值为 .
.
(1)设数列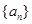 为1,3,5,7,
为1,3,5,7, ,写出
,写出 ,
, ,
,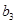 的值;
的值;
(2)若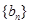 为等差数列,求出所有可能的数列
为等差数列,求出所有可能的数列 ;
;
(3)设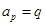 ,
, ,求
,求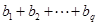 的值.(用
的值.(用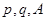 表示)
表示)
设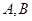 是椭圆
是椭圆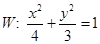 上不关于坐标轴对称的两个点,直线
上不关于坐标轴对称的两个点,直线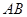 交
交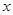 轴于点
轴于点 (与点
(与点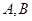 不重合),O为坐标原点.
不重合),O为坐标原点.
(1)如果点 是椭圆
是椭圆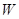 的右焦点,线段
的右焦点,线段 的中点在y轴上,求直线AB的方程;
的中点在y轴上,求直线AB的方程;
(2)设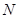 为
为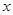 轴上一点,且
轴上一点,且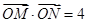 ,直线
,直线 与椭圆
与椭圆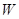 的另外一个交点为C,证明:点
的另外一个交点为C,证明:点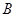 与点
与点 关于
关于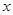 轴对称.
轴对称.
已知函数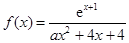 ,其中
,其中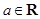 .
.
(1)若 ,求函数
,求函数 的极值;
的极值;
(2)当 时,试确定函数
时,试确定函数 的单调区间.
的单调区间.
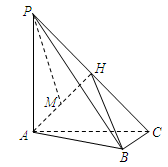
如图,在三棱锥 中,
中,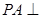 底面
底面 ,
,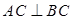 ,
,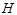 为
为 的中点,
的中点, 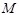 为
为 的中点,
的中点, ,
,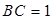 .
.
(1)求证: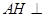 平面
平面 ;
;
(2)求 与平面
与平面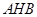 成角的正弦值;
成角的正弦值;
(3)设点 在线段
在线段 上,且
上,且 ,
, 平面
平面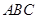 ,求实数
,求实数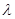 的值.
的值.